Calcule onde e é a parte da superfície com sendo a normal tal que .
Passo 1
Vamos começar com um esboço da região para entender melhor o que está acontecendo. Temos o elipsoide:
Com . É isso aqui então:
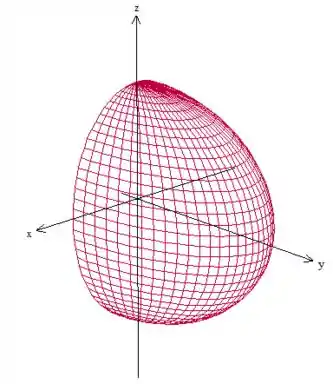
Passo 2
Como deve dar trabalho calcular isso ai pela definição (dá uma olhada no campo), vamos tentar usar Gauss aqui. Começarmos calculando esse divergente:
Olha que maravilha isso aqui.
Passo 3
Para usar Gauss, precisamos fechar essa região.Vamos fechar com esse disco (elipse) que a borda de forma, pode ser? Então, temos isso aqui:
Sendo a região na figura acima, orientada positivamente, e é a elipse que fecha . Temos então:
Onde é metade do volume do elipsoide. Lembra que o volume de um elipsoide é dado por isso aqui?
Onde são as raízes dos denominadores de , e (os semeixos do elipsoide):
Portanto:
Isso nos dá:
Passo 4
Agora precisamos da integral na elipse. Para descobrir sua equação vamos fazer na equação do elipsoide:
Vamos parametrizar isso aí em coordenadas elipticas então:
Onde e .
Lembrando que a elipse pertence ao plano . Show, agora vamos achar a sua normal:
Como a normal deve apontar para fora de , para a elipse, isso significa , portanto, queremos o vetor oposto a esse:
Passo 5
Agora, vamos usar essa fórmula aqui:
Escrevendo o campo em função da parametrização, temos:
Levando o que temos para a integral:
Passo 6
Temos então