Considere o campo vetorial
- Calcule o fluxo de através do disco dado pela interseção da esfera com o plano , orientado para cima.
- Determine o divergente de .
- Calcule o fluxo de através do pedaço da superfície esférica que se situa acima do plano , orientada pela normal exterior.
Passo 1
Letra a) Vamos começar esse problema, entendendo um pouco mais sobre o disco .
Sabemos que ele está sendo dado pela interseção da esfera , que tem raio , com o plano paralelo ao plano passando por .
Desenhando essas duas coisas juntas no espaço, teremos
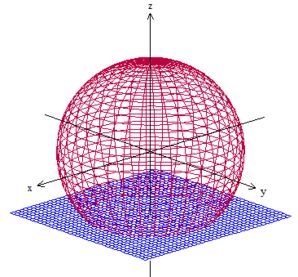
No caso, como o problema nos pediu o disco, a superfície será essa em cima do plano dentro da esfera
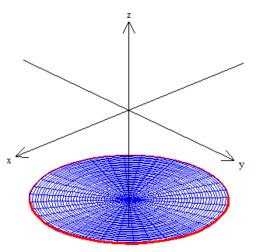
Calcular o fluxo do campo por esse disco é apara a gente aqui calcular a integral de superfície
Então vem comigo!:)
Passo 2
Antes de tudo, devemos procurar uma parametrização para a nossa superfície .
Como essa superfície é esse disco por cima do plano , podemos então pensar numa parametrização explícita:
Ou seja, uma boa parametrização para o plano é
Percebeu?
Como toda e qualquer parametrização, onde esses parâmetros e estão variando?
Bem, pra isso utilizamos a restrição: não queremos o pedaço do plano restrito dentro da esfera ? Sim! E como no plano temos , substituindo...
Ou seja, queremos e dentro da equação que representa um círculo de raio :
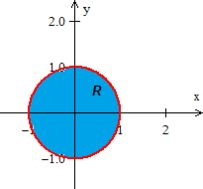
Chamamos essa região de .
Passo 3
Bem, antes de partirmos para as contas, precisamos encontrar aquele vetor normal da superfície.
Pow! Aqui, basta usar o bizu de parametrização explícita do tipo , ou seja,
Lembrando que , teremos , voltando para a integral e substituindo tudo, teremos
Fazendo esse produto interno
Agora é só calcular essa integral dupla aí e partir para o abraço!
Passo 4
Como estamos dentro de , uma região circular, vamos fazer uma mudança para coordenadas polares
Onde olhando para a região, notamos que o raio...
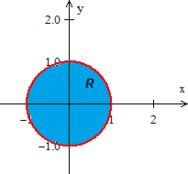
E o ângulo theta dá uma volta completa, ou seja,
Logo,
Integrando primeiro em
Lembrando que
Integrando aí lembrando que
Integrando isso aí, lembrando que pelo
Substituindo esses caras, ganharemos
Passo 5
Letra b) Para o cálculo do divergente, não tem mistério, basta aplicar a fórmula
Como , calculando essas derivadas parciais...
E jogando no divergente
Passo 6
Letra c) Então, agora devemos encontrar o fluxo através do pedaço da esfera acima do plano
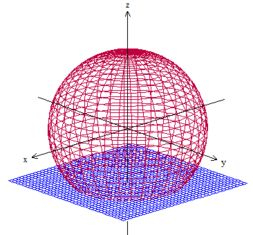
Como já determinamos o divergente, podemos tentar resolver esse problema por teorema de Gauss. Bora então?
Passo 7
Gauss nos fala o seguinte:
Esse é a borda do sólido que esta acima do plano e abaixo da esfera, ou seja, é a união do disco com (o pedaço da esfera que queremos), logo
Então, substituindo em Gauss
Mas note que essa integral , não é a mesma que calculamos, é a inversa negativa dela! What????
Calma!
Olha só, calculamos essa integral com o vetor apontando pra cima.
Como agora queremos com o vetor pra baixo (pois todos vetores devem estar saindo do sólido), apenas inverteremos o sinal, percebeu?!:)
Logo
Bem, de integral de superfície, mão tem mais nada. Basta resolver essa integral tripla aí e o nosso problema acaba!
Passo 8
Para resolver essa integral tripla no sólido : , vamos precisar prestar muita atenção, pois essa integral não é simples de se resolver, beleza?
Para facilitar, a gente vai dividir o sólido em duas partes um pouco mais fáceis:
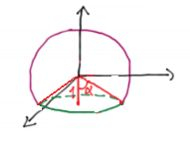
Ou seja, dividimos em um pedaço de esfera em rosa, e um cone em vermelho.
Qual que é o legal de fazer isso, é que podemos dividir aquela integral tripla em duas partes também:
- Uma integral que a gente poderá usar coordenadas esféricas (na parte da esfera rosa)
- A outra integral, na parte do cone, poderemos resolver por uma substituição cilíndrica:
onde o raio varia de até 2 , o ângulo varia de até e o ângulo varia de até o ângulo máximo que a gente vai ver qual é.
Então vamos nessa?
Passo 9
Vamos começar com o pedacinho de esfera rosa.
Sabemos que vamos usar coordenadas esféricas, mas qual é os limites dessas variáveis aí mesmo?
Bem, o raio , ele simplesmente sai da origem e vai até o raio máximo da esfera:
é aquele ângulo que varia no plano , e portanto ele deve dar uma volta completa:
Quanto ao , ele varia de cima pra baixo no eixo , então ele começa no ângulo e vem até aquela retinha vermelha.
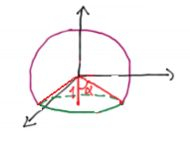
Se lembrarmos de que essa circunferência verdinha tem raio igual a 1,
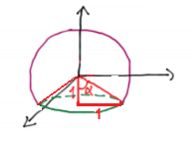
Logo esse ângulo , só pode ser de , ou · Então o ângulo
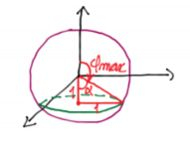
Será o seu complementar, ou seja
Logo
Passo 10
Resolvendo a integral tripla em cima dessa esfera, lembrando-se de multiplicar a função pelo jacobiano das eféricas, teremos
Substituindo pelos da parametrização e substituindo o jacobiano...
Integrando primeiro em
Substituindo os limites
Lembrando se de que ,
Simplificando
Como
Passo 11
Bem, mas infelizmente não acabou aí! Falta regressarmos na integral, mas agora fazendo para o cone vermelho utilizando a substituição cilíndrica
Uma equação que pode nos ajudar é a do cilindro
O jacobiano nessa substituição vale
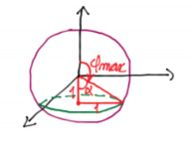
Note que esse cone ele é aquele cone normal que conhecemos de equação , porque o ângulo de abertura ali é de
Passo 12
Vamos encontrar então os limites dessas variáveis aí:
O raio , varia de ao raio máximo que é delimitado pelo cone vermelho, portanto
Como o cone é , extraindo a raiz
Bem, não se esqueça de que o cone está na parte onde é negativo, então
Quanto a , podemos perceber na figura que ele varia de até
novamente dá uma volta completa dentro do cilindro
Passo 13
Substituindo os limites na integral tripla, mas dessa vez para o cone
Integrando em primeiro
Substituindo os limites
Integrando em
Passo 14
Logo, podemos concluir então que a integral tripla no sólido inteiro, é a soma do resultado apenas na parte rosa com a parte vermelha do cone
Regressando para o teorema de Gauss do final do passo 7...
Resposta
Letra a)
Letra b)
Letra c)