Questão 4: Considere uma esfera eum paralelepípedo sólido definidos por
- Dê uma parametrização da superfície , orientada com vetor normal apontando para a origem.
- Dê duas expressões que permitam calcular o fluxo do campo através de , uma na parametrização, e outra usando o Teorema de Gauss.
- Escolha uma destas duas expressões e calcule o fluxo
Passo 1
Item I)
Primeiro é legal termos uma visão geométrica da nossa superfície, certo? Sabemos que a nossa é a intersecção da esfera de raio :
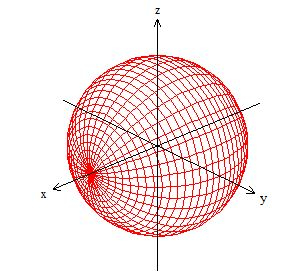
Com o paralelepípedo, onde , e :
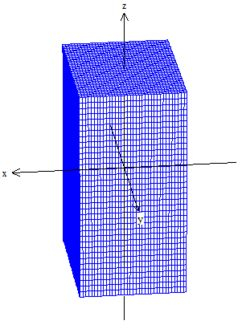
Pow, os pontos que são comuns tanto à casca esférica e o paralelepípedo, são esses pontos da esfera no interior:
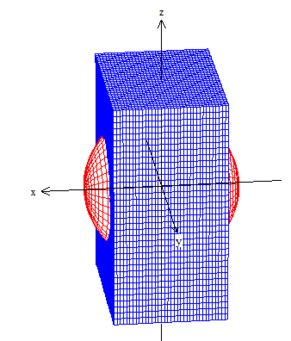
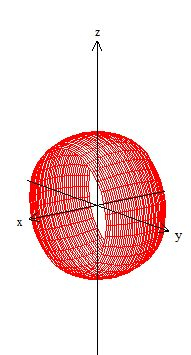
Como se tivéssemos cortado as calotas em e em e as jogadas fora, entende?
Passo 2
Parametrizar essa superfície requer a utilização das primas das coordenadas esféricas:
Só que a gente vai mudar algumas coisas nela. Bem, primeiro, perceba que com essa mudança, temos essas variáveis “variando” desse jeito aqui, veja:
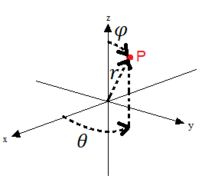
Poxa, veja que é extremamente complicado descrever o sólido com essas variáveis do jeito que esta, pois o ângulo é depende do ângulo . Mas veja que se mudarmos as coordenadas de forma que o ângulo varie da borda feita pelo plano até a outra feita pelo plano , dessa forma aqui:
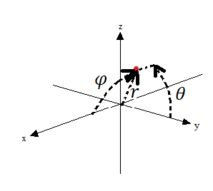
Muito melhor, pois assim, o ângulo varia de até , enquanto ângulo varia de uma borda a outra sem depender de , saca? Mas ao fazer essa mudança, estamos basicamente mudando as coordenadas:
Pra fazer essa troca, é só observar que para o ângulo sai do eixo , então temos que ter o com (o mesmo vale para o ângulo sai do eixo ), saca?
Bem, essas aí são as coordenadas esféricas, mas queremos utiliza-la para parametrizar uma esfera de raio fixo igual a , então concluímos que uma boa parametrização é:
Passo 3
Calma jovem, que ainda falta os limites!
Como já comentamos, vamos ter um ângulo dando uma volta completa ao redor do eixo :
Enquanto isso:
Onde mudando para os termos da parametrização...
E
Logo:
Passo 4
Calma que só falta mais uma coisinha para terminarmos: o vetor normal!
Esse vetor sempre pode ser encontrado fazendo o produto vetorial entre as derivadas parciais da parametrização de superfície:
Só que calcular essas derivadas parciais aí é um pouco chato! Aqui é melhor utilizar um bizu: toda vez que temos esferas centradas na origem sendo parametrizadas, basta fazermos:
Onde é o raio da esfera que no caso é :
Só tem um porem: o enunciado nos pede...
“... orientada com vetor normal apontando para a origem.”
Logo, para esse vetor normal atender essa condição, precisamos inverter o sinal dessas coordenadas aí:
Passo 5
Item II)
A primeira expressão é a integral de superfície calculada de uma forma direta:
Onde:
Em termos das parametrizações...
Enquanto isso:
E:
Então:
Passo 6
A outra expressão é proveniente do Teorema de Gauss:
Mas para isso precisamos de uma superfície fechada e sendo o bordo do sólido . Ora, essas bordas pode ser os próprios discos em e :
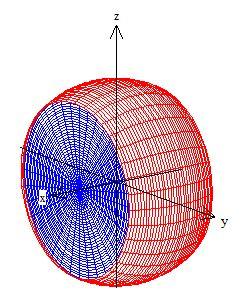
Esses discos têm equações:
A eles vamos dar o nome de para o disco no plano e para o que está no plano , assim, pelo Teorema de Gauss, a borda :
Como o divergente do campo é...
Ficamos com...
Passo 7
Item III)
Vamos escolher essa primeira opção, pois parece ser mais tranquila:
Como ...
Colocando as integrais dentro de uma só...
Fazendo uma mudança:
Mudando também os limites...
Então...
Resposta
Item I)
Item II)
Item III)