A figura mostra uma barra retilínea condutora, de massa , comprimento e resistência elétrica , movendo-se com uma velocidade constante ao longo de trilhos condutores, retilíneos horizontais, fixos.
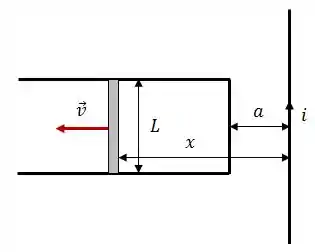
Tal circuito está sob ação de um campo magnético gerado por uma corrente elétrica estacionária fluindo por um fio retilíneo longo, paralelo à barra e no mesmo plano do circuito.
A resistência dos trilhos, assim como a capacitância e a autoindutância do circuito e a indutância mútua entre o circuito e o fio retilíneo (de corrente ) podem e devem ser desprezadas.
Obtenha uma expressão para a corrente elétrica no circuito, , como função da distância da barra ao fio.
[Sugestão: não precisa deduzir o campo magnético de uma corrente retilínea estacionária, muito longa.]
Obtenha uma expressão para a taxa temporal de dissipação de energia, pelo efeito Joule, na barra, como função de .
Obtenha uma expressão para a força externa que precisa ser aplicada à barra para manter a sua velocidade constante.
Passo 1
Obtenha uma expressão para a corrente elétrica no circuito, , como função da distância da barra ao fio.
Vamos por partes... Para calcular a corrente elétrica no circuito, primeiro vamos ter que calcular a induzida , de forma que:
A induzida, de acordo com a lei de Faraday, é dada por:
Então vamos precisar calcular o fluxo magnético, definido por:
Mas antes, teremos que encontrar a expressão do campo magnético gerado pelo fio de corrente , que é calculado através da lei de Ampère, dada por:
Então, no fim, serão mais 4 passos... Viu o tamanho do drama?
Mas nós damos conta!
Passo 2
Por conta da simetria do problema, a amperiana será uma circunferência de raio , logo:
Pela regra da mão direita, na região da espira, o campo magnético está saindo do plano da página.
Passo 3
O elemento de área será dado por:
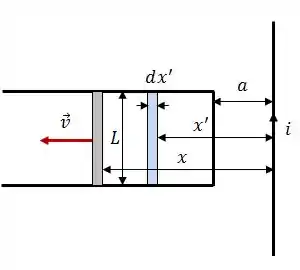
Portanto:
Passo 4
Pela Lei de Faraday:
Passo 5
A corrente será dada por:
Passo 6
Obtenha uma expressão para a taxa temporal de dissipação de energia, pelo efeito Joule, na barra, como função de .
A “taxa de dissipação de energia” é a mesma coisa que “potência dissipada”, que é dada por:
Logo:
Passo 7
Obtenha uma expressão para a força externa que precisa ser aplicada à barra para manter a sua velocidade constante.
Para manter a barra com velocidade constante, a força externa deve ter a mesma direção da força magnética sobre a barra, o mesmo sentido, porém sentidos opostos, de forma que:
A força magnética sobre a barra é dada por:
Logo:
Substituindo o a expressão de , teremos:
Portanto:
Resposta