Uma semente de melancia possui as seguintes coordenadas: e . Determine o vetor posição da semente na notação de vetores unitários e como um módulo e um ângulo em relação ao sentido positivo do eixo . Desenhe o vetor em um sistema de coordenadas dextrogiro. Se a semente é transportada até as coordenadas determine seu deslocamento na notação de vetores unitários e como um módulo e um ângulo em relação ao sentido positivo do eixo .
Passo 1
A notação de vetor unitário, basta colocar as coordenadas para representar os eixos respectivamente.
no início a semente de melancia possuía as coordenadas , e que vão ser as posição
, e do vetor
Então o vetor posição fica:
Passo 2
Vamos fazer o módulo de
Substituindo os valores temos:
Passo 3
Para achar o ângulo entre dois vetores, vimos uma fórmula, como queremos encontrar o ângulo entre o vetor e o eixo positivo, vamos encontrar o ângulo do vetor com um vetor que esteja na direção do positivo.
Então vamos achar o vetor que representa o sentido positivo do eixo , que é o vetor unitário , onde :
De módulo 1
Assim podemos aplicar a fórmula do ângulo entre dois vetores
Já temos os módulos dos dois vetores, basta acharmos o valor do produto escalar entre eles e calcularemos esse valor por essa fórmula
Substituindo todos os valores encontrado na equação do ângulo temos
Passo 4
Primeiro, o que é um sistema de coordenadas dextrogiro??
É simplesmente isso:
Como as coordenadas no eixo são zero, podemos para simplificar o desenho desenhar em duas dimensões
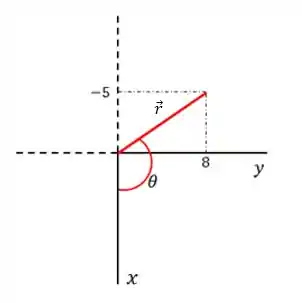
O ângulo theta do desenho é o ângulo encontrado anteriormente .
Passo 5
O vetor deslocamento é dado por
Substituindo a posição inicial e a final teremos
Passo 6
O modulo de é
Passo 7
Como fizemos no item vamos primeiro achar o produto escalar entre e
Assim podemos aplicar a fórmula do ângulo entre dois vetores
Substituindo todos os valores na equação do ângulo temos
Resposta