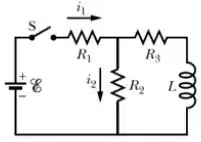
. No circuito da figura abaixo, , , , e
. Determine os valores de e logo após o fechamento da chave .
Determine os valores de e muito tempo após o fechamento da chave.
Passo 1
Vem comigo resolver esse problema!
Nós temos em mãos um problema envolvendo circuito .
Sobre esse tipo de circuito temos que quando temos uma variação muito alta de corrente (quando a chave é fechada por exemplo) o indutor funciona como um circuito aberto, logo ele não participa inicialmente do circuito.
Depois de um tempo quando a corrente se estabiliza e o indutor funciona como um fio comum, ele não interfere em nada no circuito. Com isso temos um circuito com a bateria e três resistências sendo e em paralelo e em série com a equivalente de e .
E é com isso que vamos encontrar o que cada item pede.
Passo 2
No item ele quer as correnetes e no instante logo após o fechamento da chave.
Como nesse instante o indutor faz com que não passe corrente pelo ramo do circuito dele, a resistência não interfere no circuito, com isso podemos considerar apenas a bateria e e como parte do nosso circuito.
Com isso temos que , usando a lei de Ohm temos que:
Essa resistência equivalente como e estão em série, vale:
Assim temos que:
Logo temos que:
Passo 3
Agora para o item temos a situação de ter passado muito tempo depois do fechamento da chave, logo nosso indutor funciona apenas como um fio no circuito.
Vamos então primeiro encontrar a resistência total do circuito pois assim conseguimos usar a lei de Ohm para o circuito inteiro e descobrir a corrente total.
Primeiro vamos achar a resistência equivalente entre e , como elas estão em paralelo, temos que:
Assim a resistência total é dada por:
Substituindo os valores que conhecemos, temos:
Logo temos que:
Passo 4
Agora que temos a resistência total vamos encontrar a corrente total do circuito, usando a lei de Ohm, temos:
Olhando o circuito podemos ver que essa corrente total é igual a antes dela se dividir para e a corrente que passa por .
Para achar vamos analisar a situação. A potencial de potencial total do circuito é igual a e levando em conta de que como e estão em paralelo suas diferenças de potencial são iguais, então temos que:
Substituindo o que sabemos, temos:
Então temos que a diferença de potencial em vale , usando a lei de Ohm, temos:
`Prontinho, temos tudo o que ele queria.