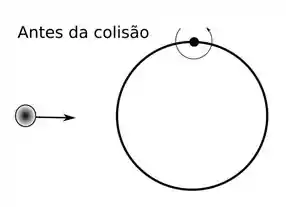
Um aro rígido de raio e massa está deitado sobre uma mesa sem atrito e é articulado num ponto . Um objeto pontual de massa tem velocidade para a direita numa trajetória diametral de aro. Ele colide elasticamente com o aro. Depois da colisão, o objeto está retornando para a esquerda com velocidade e o aro passa a rodar com velocidade angular . O momento de inércia do aro por um eixo através do seu centro e perpendicular ao plano do aro é .
Qual é a velocidade do objeto depois da colisão? Expresse sua resposta em função das variáveis do exercício. Não use em sua resposta.
Passo 1
E aí galerinhaaaaa, como vocês estãooo?
Nessa questãozita temos um probleminha envolvendo colisões. Basicamente, temos um aro articulado em um de seus pontos, que está tranquilão lá, parado, quando de repente um objeto pontual com velocidade se choca com ele.
A partir disso, o aro começa a girar com velocidade e objeto retorna com velocidade .
O enunciado nos pede para determinar em função das outras variáveis.
E aí, o que podemos fazer aqui?
Gente, como tem colisão envolvida a ideia geral vai ser usarmos a conservação do momento linear e conservação da energia mecânica(pois a colisão é elástica). Assim, vamos ter duas equações e duas incógnitas e .
Tranquilo?
Então vamo nessa!!
Passo 2
Vamos começar pela conservação do momento linear. Como não há forças externas atuando na direção da colisão, podemos dizer que o momento linear irá se conservar.
Inicialmente, o aro está parado, então o momento linear deve-se apenas ao objeto pontual:
Massa!
Após a colisão, o objeto retorna com velocidade . Então:
O sinal de negativo é porque o momento linear é uma grandeza vetorial, e a velocidade do objeto inverteu o seu sentido após a colisão. Teremos também momento linear no aro, onde a velocidade é a velocidade do centro de massa:
Como o aro vai girar em torno da articulação com , podemos dizer que:
Logo:
Juntando tudo:
Pela conservação do momento linear, podemos igualar seus valores antes e após a colisão. Assim:
Daí:
Show! Conseguimos a primeira equação.
Passo 3
Agora vamos trabalhar com a ideia de conservação da energia mecânica.
Inicialmente, tínhamos apenas o objeto pontual em movimento, e a energia cinética vale:
Após a colisão, tanto o objeto como o aro estão se movimentando (objeto transladando e o aro girando). Asism:
é o momento de inércia relativo ao eixo de rotação. Então, precisaremos usar o teorema dos eixos paralelos.
onde é momento de inércia com relação ao eixo de interesse, o momento de inércia em relação ao CM e a distância entre os eixos.
Logo:
Assim:
Igualando a energia cinética inicial e final, temos:
Muito bom!
Passo 4
Agora que encontramos duas equações, caímos num sisteminha:
Isolando na primeira equação e elevando ao quadrado, temos:
Substituindo na segunda equação, vemo:
Logo:
Cancelando termos que aparecem em ambos os lados:
Por fim:
Daí:
Ufaaa! Conseguimos 😊
Deu muito trabalho mas saiu!!
Valeu gente!