UFPE – Geometria Analítica – 2019.2 – P1 – Questão 1
Seja um paralelepípedo reto, com bases os quadrados e , de aresta , e arestas laterais , , , medindo .
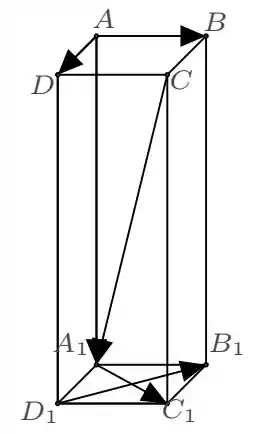
- Escreva os vetores , , como combinação linear dos vetores , e .
- Se são as coordenadas de na base , explique porque . Em seguida, calcule (corretamente!) a norma do vetor .
- Calcule o produto misto .
Passo 1
- Bora lá! Vamos usar a regra do triângulo pra mexer nesses vetores aí! Depois de usar a regra do triângulo, a gente usa a figura pra relacionar os vetores que aparecem com os vetores que a gente quer.
- Se liga! No item anterior, a gente achou:
- Nossa missão é calcular o produto misto . Bom, pra começar, vamos começar botando em função dos vetores que conhecemos. Presta atenção na figura pra cada passo!
Beleza, fechou!
Passo 2
Então, na base ,
Daqui, a gente encontra . Mas se a gente calcular a norma usando a definição, vamos encontrar:
Os três vetores são ortogonais, e então os produtos escalares vão ser todos zero. Sobre então os quadrados dos módulos, que a gente vai achar na figura!
Ué, deu diferente... Que houve? É o seguinte: essa parada de só serve para uma base ortonormal! Só que a nossa base não é ortonormal, já que , ela é só ortogonal! Essa fórmula aí nos dá na real a soma dos quadrados das coordenadas, que só vão ser a norma ao quadrado no caso de base ortonormal. Por isso a fórmula “em coordenadas” não funciona.
Passo 3
Vamos chamar de , pra facilitar pra gente perceber uma parada em seguida.
Isso pode ser separado em:
A primeira parcela é nula, já que repete vetores! Vamos ficar só com a segunda parcela, então.
Vamos desmembrar essa parada de novo!
Trocando a ordem dos termos, troca o sinal.
e são perpendiculares entre si, e, pela regra da mão direita, tem o mesmo sentido que . Como , e como tem módulo , e já que estão no mesmo sentido, o produto escalar é o produto dos módulos,
Resposta
- Essa expressão só vale para uma base ortonormal, mas essa é apenas ortogonal.