Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Movimento Harmônico Amortecido

Ver Teoria
Exercício 5012345678910111213141516171819202122232425262728293031323334353637383940414243444546474849515253545556575859606162636465666768

Enunciado

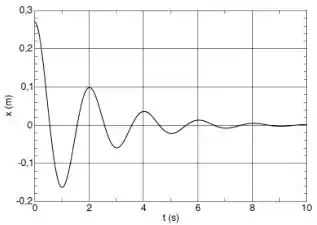
A figura mostra a posição de um sistema massa-mola sujeito à ação de uma força dissipativa proporcional à velocidade. Sabendo que a massa do bloco é m = 1,0 kg, pode-se afirmar que (dica: considere φ = 0 e lembre-se que e ≃ 2,7 e l n ( e ) = 1 ):

  1. A constante de amortecimento é γ ≃ 1   r a d   s - 1 e a frequência natural de oscilação é ω 0 ≃ 2 π   r a d   s - 1 .
  2. A constante de amortecimento é γ ≃ 1   r a d   s - 1 e a frequência natural de oscilação é ω 0 ≃ 2 π   r a d   s - 1
  3. A constante de amortecimento é γ ≃ 1   r a d   s - 1 e a frequência natural de oscilação é ω 0 ≃ π   r a d   s - 1
  4. A constante de amortecimento é γ ≃ 2   r a d   s - 1 e a frequência natural de oscilação é ω 0 ≃ π / 2     r a d   s - 1
  5. A constante de amortecimento é γ ≃ 2   r a d   s - 1 e a frequência natural de oscilação é ω 0 ≃ π   r a d   s - 1

Passo 1

Se olharmos o gráfico, vemos uma oscilação que vai decaindo exponencialmente, ou seja, um movimento harmônico amortecido (MHA).

Só que existem 3 tipos de MHA: supercrítico, crítico e subcrítico.

Como o gráfico tem uma oscilação junto com uma exponencial, então ele é obrigatoriamente subcrítico, que tem equação:

x t = A   e - γ 2 t   c o s ⁡ ( ω t + ϕ )

Onde

ω = ω 0 2 - γ 2 4

Passo 2

Primeiro vamos botar ϕ = 0 , como o enunciado nos diz.

Agora vamos olhar para o gráfico para tentar tirar informações.

Repare que a distância entre dois máximos consecutivos é de 2 s, isso quer dizer que o período

T = 2 s

Então a frequência angular

ω = 2 π f = 2 π T = 2 π 2 = π

E podemos olhar a amplitude, o ponto máximo de todo o gráfico, em t = 0 ,

A ≅ 0,27 m

Temos a equação, então:

x t = 0,27   e - γ 2 t c o s ⁡ ( π t )

Passo 3

Falta descobrir quem é o γ na equação. Para isso é só pegar o valor de x ( t ) em um ponto qualquer e substituir. Por exemplo, dá pra tirar do gráfico que

x t = 2 s = 0,1   m

Então,

x 2 = 0,1 = 0,27   e - γ 2 2   c o s ⁡ ( π ∙ 2 )

e - γ = 0,1 0,27   c o s ⁡ ( 2 π ) = 1 2,7

Como e ≅ 2,7 , então

e - γ ≅ 1 e = e - 1

Então, a constante de amortecimento,

γ ≅ 1   r a d / s

Passo 4

Para descobrir a frequência natural de oscilação ω 0 , vamos usar a relação encontrada anteriormente:

ω = ω 0 2 - γ 4

π = ω 0 2 - 1 4

Elevando ao quadrado dos dois lados:

π 2 = ω 0 2 - 1 4

ω 0 = π 2 + 1 4

Como π 2 ≫ 1 / 4 , então podemos aproximar

ω 0 ≅ π 2 = π   r a d / s

Resposta

(c) A constante de amortecimento é γ ≃ 1   r a d   s - 1 e a frequência natural de oscilação é ω 0 ≃ π   r a d   s - 1 .

Exercícios de Livros Relacionados

137. Uma máquina de 200k g se apoia sobre quatro suportes no chão, cada um dos quais possui uma constante de mola efetiva k = 250k N / m e um coeficiente de amortecimento viscoso efetivo c = 1000 N ⋅
138. Represente graficamente a resposta x do corpo de 20k g ao longo do intervalo de tempo 0 ≤ t ≤ 1 segundo. Determine os valores máximo e mínimo de x e seus respectivos instantes de tempo. As condiç
Para uma criança em um balanço, a amplitude cai em um fator de 1 e em cerca de oito períodos, se nenhuma energia mecânica adicional for fornecida ao sistema. Estime o fator Q para este sistema.
Para o cilindro do Prob. 8/8, determine o deslocamento vertical x, medido para baixo no sentido positivo em milímetros, a partir da posição de equilibro, em termos do tempo t, em segundos, medido a pa
Em um oscilador amortecido com m = 250 g , k = 85 N / m e b = 70 g / s , qual é a razão entre a amplitude das oscilações amortecidas e a amplitude inicial após 20 ciclos?