Sejam os vetores . Calcular o valor de para que a área do paralelogramo determinado por seja igual a .
Passo 1
O enunciado nos pede o valor de para que o paralelogramo formado por tenha área de .
Como eu acho o ?

Bem, nós sabemos que a área do paralelogramo formado pelos vetores é . Sabemos pela teoria que o módulo do produto vetorial é a área do paralelogramo. Então, fazemos o produto vetorial e depois calculamos o módulo para achar ;).
Passo 2
Então, vamos calcular primeiro o produto vetorial:
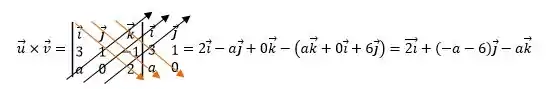
Passo 3
Temos o vetor resultante do produto vetorial, então agora é só calcularmos o módulo:
Resolvendo a equação de 2º grau, chaga-se em: