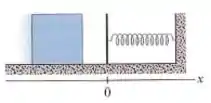
Um bloco de massa desliza para a direita de encontro a uma mola de constante elástica . Quando atinge a mola, a velocidade do bloco é igual a . O bloco para momentaneamente após comprimir a mola de . Qual é o módulo da força de atrito exercida pelo piso sobre o bloco?
(A)
(B)
(C)
(D)
(E)
Passo 1
Para resolver essa questão, utilizaremos o famoso teorema trabalho-energia cinética:
Lembrando que nesse teorema, usamos o trabalho resultante. Então, ele será a soma do trabalho de todas as forças atuando sobre ele.
Como a força peso e normal são perpendiculares ao deslocamento, seus trabalhos são nulos, restando apenas o trabalho da força de atrito e da força elástica:
Queremos encontrar a força de atrito.
Passo 2
Já temos as informações sobre a compressão da mola, sua velocidade inicial e sobre a constante elástica da mola. Vamos calcular o trabalho e a variação de energia cinética .
O trabalho da força elástica é:
Mas repara que o movimento está contra a força da mola, então seu trabalho na verdade é negativo:
Já a variação de energia cinética é:
Passo 3
Juntando o que calculamos na expressão, temos:
O trabalho da força de atrito é:
Então:
O deslocamento será exatamente o quanto a mola deformou, portanto:
Resposta
Letra (B)