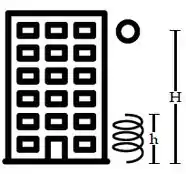
Um objeto de massa é largado do repouso de um prédio a uma altura em relação ao solo. Uma mola ideal foi colocada no solo para suavizar a desaceleração do objeto. Esta mola possui uma constante elástica e um comprimento quando não está deformada. Dado: .
(a) Determine o trabalho realizado pela força peso até o instante de contato entre o objeto e a mola.
(b) Desprezando a resistência do ar, qual deve ser a constante elástica da mola para que o objeto pare momentaneamente a uma altura em relação ao solo?
(c) Considerando agora o efeito da resistência do ar durante a queda, observa-se que o objeto inicia o contato com a mola a uma velocidade . Qual é o trabalho realizado pela força de resistência do ar durante a queda até o instante em que o objeto inicia o contato com a mola?
Passo 1
Na letra (a), queremos o trabalho da força peso da posição inicial do objeto (alto do prédio) até a posição onde o objeto atinge a mola.
Podemos calcular o trabalho da força peso com o produto interno da força peso com o deslocamento:
Onde o ângulo é o ângulo entre os dois vetores.
Mas, ta vendo que esses vetores apontam na mesma direção?
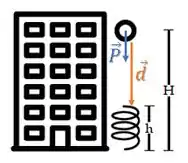
Então:
Ou seja, o produto interno fica apenas o módulo dos dois vetores:
Tá vendo que o sinal deu positivo?
Beleza, isso realmente é para acontecer quando a força está a favor do deslocamento.
Passo 2
Agora, devemos tomar cuidado em quem é esse deslocamento .
Ele será a diferença entre a altura do prédio e a altura da mola
Logo:
Passo 3
Na letra (b), queremos a constante da mola que faça com que o objeto após a queda perca velocidade e pare a uma altura de do chão.
Agora, vamos pensar...
Se desprezamos a resistência do ar, conseguimos achar a velocidade do objeto após a queda de , posição na qual a mola passa a atuar.
Porém, a força da mola não é constante, ela varia conforme a deformação. Assim, fica mais difícil resolver por cinemática com aquelas equações de movimento.
Uma boa alternativa é pensar em energia...
Durante a queda, apenas a força peso e a elástica atuam sobre o objeto. Como ambas são forças conservativas (não retiram energia do sistema), podemos dizer que a energia mecânica do sistema se conserva.
Assim, podemos relacionar o momento inicial com o momento final considerando as energias envolvidas em cada um deles.
Passo 4
Beleza, vamos considerar como momento inicial, o momento em que o objeto é largado do alto do prédio.
Como ele parte do repouso, sua velocidade é nula, portanto não há energia cinética . Porém, ele terá uma energia potencial gravitacional associada à sua altura .
Enquanto que o momento final será quando ele finalmente parar pela ação da mola.
Assim, novamente sua energia cinética será nula, entretanto, ele terá tanto energia potencial gravitacional relacionada à sua altura , quanto energia potencial elástica associada à deformação da mola:
Mas quem será a deformação da mola ?
Passo 5
Como a mola relaxada tem uma altura de do chão, se o objeto tem que parar a uma altura de , a mola deformou :
Passo 6
Agora, podemos voltar à equação da conservação e achar o valor da constante elástica da mola que apareceu alí na sua energia potencial:
Vamos substituir os valores:
Putz não tava lembrando dessa unidade de ...
Só a gente conferir olhando para a fórmula da força elástica:
Como a força elástica é dada em Newtons e a deformação da mola é dada em metros , nada mais justo que a constante elástica seja dada em .
Passo 7
Na letra (c), ele diz que há uma resistência do ar.
A resistência do ar, como o próprio nome já diz, é uma força que age contra o movimento, ou seja, retirando energia.
Essa força acaba realizando um certo trabalho e diminuindo a velocidade da bola.
Portanto, a bola chega à mola com uma velocidade menor do que ela teria caso não tivesse resistência do ar.
Beleza, mas como achamos esse trabalho da resistência do ar?
Trabalho de uma força é dado por:
Entretanto, apesar de sabermos o deslocamento, não sabemos o módulo da força de resistência do ar .
Então, temos que pensar em um outro caminho.
Repara que temos a velocidade inicial e final do movimento do objeto. Assim, podemos relacionar o trabalho resultante com a variação de energia cinética por meio do teorema:
Passo 8
Mas quem é o trabalho resultante?
Ele será a soma de todos os trabalhos sobre o objeto (peso e resistência do ar):
A energia cinética inicial é zero, já que o objeto parte do repouso. Além disso, já calculamos o trabalho da força peso ao longo desse deslocamento e sabemos conseguimos calcular as energias cinéticas a partir das velocidades:
Substituindo o valor da velocidade, temos:
Opaaa, trabalho negativo???
Isso mesmo, lembra que a força age contra o movimento?
Então, seu trabalho será negativo.
Resposta
(a)
(b)
(c)