[Enunciado comum às Questões 3 e 4]
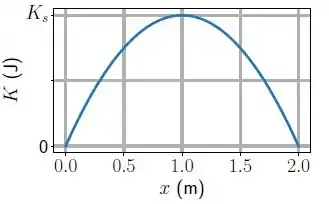
Um bloco de massa repousa em uma superfície horizontal sem atrito e está preso a uma mola de constante elástica e massa desprezível. A extremidade oposta da mola é mantida presa a uma parede. O bloco está em repouso na posição em que a mola está relaxada (). Nesta situação uma força constante ́é aplicada no sentido positivo do eixo . A figura mostra o gráfico da energia cinética do bloco em função da posição após a aplicação da força. Considere .
[Questão 4]
O módulo da força ́é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Bom, para encontrar essa força , temos o gráfico como informação numérica.
Como podemos relacionar essa força com a energia cinética?
Podemos usar o Teorema Trabalho-Energia Cinética:
Onde o trabalho resultante vai ser o trabalho de todas as forças atuando no sistema.
Passo 2
Quais são as forças sobre o bloquinho?
Temos a força peso e normal na vertical, além disso, a força puxando o bloco e a força elástica contrária ao “esticamento” da mola.
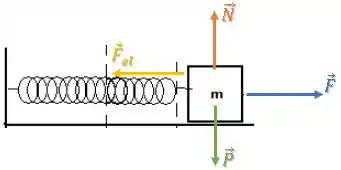
Então, o trabalho resultante vai ser:
Nossa! Quatro trabalhos para calcular ☹
Calma, logo de cara temos que tanto o trabalho da força peso quanto o trabalho da força normal serão nulos, já que eles são perpendiculares ao deslocamento do bloco.
Então, ficamos com isso aqui:
Passo 3
A força está na mesma direção e sentido do deslocamento, logo seu trabalho será positivo e dado por:
Já a força elástica está no sentido oposto ao do deslocamento, então seu trabalho será negativo e dado por:
Assim, ficamos com:
Vamos considerar a posição inicial como e a posição final como , para podermos usar o dado numérico do gráfico. Assim, temos que o deslocamento será de metro:
Opa, mas temos o problema de não conhecermos o valor da constante elástica da mola .
Passo 4
Assim, vamos achar mais uma relação entre e para conseguirmos resolver esse problema.
Para essa relação, vamos usar aquele ponto de energia cinética máxima alí:
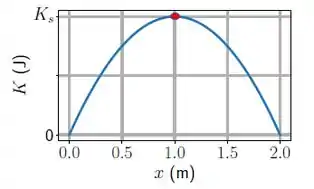
Por que esse ponto?
Bom, porque antes dele a energia cinética estava aumentando (velocidade aumentando), ou seja a força resultante estava no sentido do movimento.
Enquanto isso, depois desse ponto a energia cinética está diminuindo (velocidade diminuindo), ou seja, a força resultante está contrária ao movimento.
E exatamente sobre esse ponto??
Se esse ponto é a transição dessas duas situações que vimos, então sobre ele a força resultante é nula:
Ou seja, a força elástica está equilibrando a força :
Pronto, está ai a nossa segunda relação.
Passo 5
Usando que na primeira relação, ficamos com:
Ficamos com a letra (e).
Resposta
Letra (e)