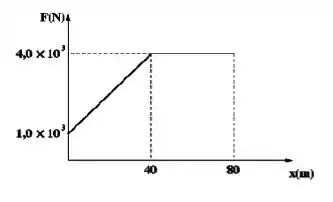
Um grande bloco de massa se movimenta horizontalmente através de uma distância total de sobre um piso com atrito a partir do repouso. Um trator empurra o bloco durante os primeiros com uma força variável, descrita pelo gráfico abaixo:
Dado: (capa da prova)
(a) Calcule o trabalho total realizado pelo trator sobre o bloco.
(b) Ao final dos 100 𝑚, o bloco chega ao repouso. Encontre o coeficiente de atrito cinético entre o bloco e o piso.
(c) Ache a velocidade do bloco na posição 𝑥=80 𝑚.
Passo 1
Temos um bloco sendo empurrado por um trator que exerce uma força ao longo do trajeto.
Na letra (a), queremos o trabalho do trator sobre o bloco nesses primeiros nos quais o bloco anda sobre ação da força .
Passo 2
Para achar o trabalho do trator sobre o bloco, podemos pensar em calcular a partir de:
Onde o é o deslocamento.
Porém, qual seria o módulo de que colocaríamos na fórmula?
Como a força varia ao longo do trajeto, teríamos que encontrar um valor médio de .
Então, é melhor usar uma outra estratégia para calcular o trabalho de uma força variável. Vamos usar a nossa queridinha (só que não) integral:

Calma, não se assuste com a integral, ela não morde. Na verdade, só um poquinho de vez em quando hahah.
A ideia da integral é calcular para cada valor de o trabalho exercido sobre o bloco em um deslocamento muito pequenininho e somar tudo isso que no final temos o trabalho total ao longo do trajeto.
Passo 3
Mas, fica tranquilo, como a integral têm o mesmo valor da área abaixo do gráfico, podemos simplesmente calcular essa área total que conseguimos o valor de .
Então, vamos dividir aquela área alí em um trapézio e um retângulo para facilitar:
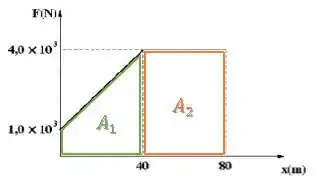
A área total será a soma dessas duas áreas:
O e são as bases maior e menor do trapézio, é a base do retângulo, enquant (horizontal) e (vertical) são as alturas:
Então, achamos o trabalho do trator sobre o bloco:
Passo 4
Na letra (b) queremos, o coeficiente de atrito entre o chão e o bloco.
Mas como achamos isso?
Precisamos primeiro saber o valor da força de atrito atuando no bloco para depois achar o coeficiente de atrito :
E como achamos essa força de atrito?
Passo 5
Podemos tentar usar aquela informação que achamos na letra (a), afinal quase sempre as questões pedem coisas que estão relacionadas com o item anterior, né.
Você concorda comigo que se o bloco começou em repouso e terminou em repouso, nesse meio tempo, o trabalho (energia) que o trator fez sobre o bloco tem que ser o mesmo trabalho (energia) que a força de atrito “tirou” desse sistema?
Essa é a ideia daquele teorema trabalho-energia cinética:
Se a variação de energia cinética foi nula entre o instante inicial e final, temos que:
Beleza, vamos partir disso agora.
Passo 6
Como a força de atrito está contra o deslocamento, seu trabalho será negativo, além disso a força é constante em todo o trajeto, então podemos escrever seu trabalho como:
Logo:
Passo 7
Quem vai ser essa força Normal ?
Como o bloco está em equilíbrio vertical, podemos dizer que a força normal vale a mesma coisa que a força peso:
Então:
Vamos substituir os valores que temos:
Achamos que o coeficiente de atrito é:
Passo 8
Na letra (c), queremos a velocidade do bloco na posição , ou seja, depois que a força terminou de exercer aquele trabalho que calculamos na letra (a).
Novamente, podemos aplicar o teorema trabalho-energia cinética:
Mas agora, conseguimos calcular os trabalhos das forças e queremos achar a energia cinética final, assim, encontramos a velocidade do bloco.
Passo 9
Como o bloco parte do repouso, sua energia cinética inicial é zero:
Então, a soma dos trabalhos com será igual a:
Passo 10
Vamos calcular o trabalho da durante o deslocamento de à :
Passo 11
Jogando o valor do e de na nossa expressão, temos:
Agora, vamos descobrir a velocidade :
Resposta
(a)
(b)
(c)