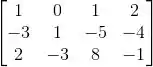Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios de Imagem e Sobrejetividade de uma Matriz - Lista de Exercícios Resolvida

Ver Teoria

Questão 1

Considere o sistema A x = b

  1. Se não tem solução, então b ___ ( ∈ , ∉ ) ____ ( I m A ,   N u c A )
  2. Se a solução não é única, então N u c ( A ) ____ ( = , ≠ ) _____ ( I m A , 0 )

Ver solução completa

Questão 2

Considere as afirmativas abaixo sobre A x = b , um sistema linear com duas equações incompatíveis.

  1. A não é sobrejetiva
  2. A pode ser injetiva
  1. Ambas são falsas
  2. I é falsa e II é verdadeira
  3. Ambas são verdadeiras
  4. I é verdadeira e II é falsa

Ver solução completa

Questão 3

Qual das matrizes abaixo possui imagem contida no plano x + y + z = 0 ?

( a ) 1 - 1 1 1 1 - 1 - 1 1 1

( b ) 1 2 3 1 2 3 1 2 3

( c ) 1 1 - 2 - 1 1 0 1 - 1 0

( d ) 1 - 1 1 1 1 - 1 - 2 0 0

Ver solução completa

Questão 4

Seja a matriz F = 1 2 1 3 1 1 2 - 1 0 .

Calcule a imagem, o posto, o núcleo e sua dimensão de F .

Ver solução completa

Questão 5

Assinale a matriz cujo núcleo é a reta x - 2 y = 0 e cuja imagem está contida no plano x + y + z = 0

a   A = 1 - 2 1 - 2 4 - 2

b   A = 1 - 2 - 2 4 0 0

c   A = 1 - 2 0 - 2 4 0

d   A = 1 - 2 - 2 4 1 - 2

Ver solução completa

Questão 6

Seja A uma matriz n × k e B uma matriz n × n .

Suponha que a imagem de A está contida no núcleo de B .

Então podemos dizer que:

a   B A é injetiva

b   B A é sobrejetiva

c   B A = I

d   B A = 0

Ver solução completa

Questão 7

Seja A uma matriz 2 × 3 apenas com entradas 0 ou 1 . Se I m A = { x - y = 0 } e N u c A = { x + y + z = 0 } , qual a soma das entradas de A ?

a   0

b   4

c   6

d   Não há informações suficientes para se determinar

Ver solução completa

Questão 8

Sejam A , B e C matrizes tais que C = A B . Considere as afirmativas:

  1. Se A é injetiva e B não é injetiva, C pode ser injetiva.
  2. Se A é sobrejetiva e B não é sobrejetiva, C pode ser sobrejetiva.

a   A afirmativa I é falsa e a afirmativa I I é falsa

b   A afirmativa I é verdadeira e a afirmativa I I é falsa

c   A afirmativa I é falsa e a afirmativa I I é verdadeira

d   A afirmativa I é verdadeira e a afirmativa I I é verdadeira

Ver solução completa

Questão 9

Seja A x → = b → um sistema linear m × n qualquer. Considere as seguintes afirmações:

I   Se a dimensão do espaço gerado pelas colunas de A é menor do que m então não pode haver A x → = b → sem solução.

I I Se a dimensão do núcleo de A for diferente de zero, então A x → = b → pode ter solução única.

Qual das opções abaixo é CORRETA?

( a ) A afirmativa I é verdadeira e I I é falsa.

( b ) A afirmativa I é falsa e I I é falsa.

( c ) A afirmativa I é verdadeira e I I é verdadeira.

( d ) A afirmativa I é falsa e I I é verdadeira.

Ver solução completa

Questão 10

Seja A a matriz:

1 0 - 1 1 - 1 2 3 3 0 1 1 2 1 3 2 7

Qual dos vetores abaixo não está na imagem de A ?

( a ) - 3,5 , 1,0

( b ) 0,2 , 1,3

( c ) 2 , - 4 , - 1 , - 1

( d ) - 2,4 , 6,6

Ver solução completa

Questão 11

Considere o sistema A x = b e sejam respectivamente p e q os números de colunas linearmente independentes L I de A e da matriz aumentada A b . Assinale a afirmativa VERDADEIRA:

( a ) Se p = q então o sistema tem solução única

( b ) Se p = q então o sistema não tem solução

( c ) Se p < q então o sistema possui infinitas soluções

( d ) Se p < q então o sistema não tem solução

Ver solução completa

Questão 12

Seja A = 1 2 0 2 1 3 3 2 4 e seja H a imagem de A . Assinale a alternativa verdadeira:

( a ) 1,2 , 0 , 2,1 , 3 , 3,2 , 4 é base de H .

( b ) 1,2 , 3 , 2,1 , 2 , 0,3 , 4 é base de H .

( c ) H é gerado por 1,2 , 0 , 2,1 , 3 e 3,2 , 4 .

( d ) H é gerado por 1,2 , 3 ,   2,1 , 2 e 0,3 , 4 .

Ver solução completa

Questão 13

Assinale uma base para a imagem da matriz 1 2 3 2 4 6 3 6 8

(a) { 1,0 , 0 ,   0,0 , 1 }

(b) { 1,0 , 1 ,   0,0 , 1 }

(c) { 1,2 , 3 ,   2,4 , 6 }

(d) { 2,4 , 6 ,   3,6 , 8 }

Ver solução completa

Questão 14

Seja A uma matriz 3   ×   2 . Então o núcleo de A e a imagem de   A são subconjuntos, respectivamente, de:

(a) R 3 e R 2

(b) R 2   e R 3

(c) R 3 e R 3

(d) R 2   e R 2

Ver solução completa

Questão 15

Seja A   uma matriz 4   ×   3 :

I - N ( A ) pode ter dimensão maior do que I m ( A )

II -   N A ⊂   R 3 e   I m A ⊂ R 4

(a) I é falsa e II é verdadeira

(b) Ambas são verdadeiras

(c) I é verdadeira e II é falsa

(d) Ambas são falsas

Ver solução completa

Questão 16

Assinale o conjunto que NÃO É uma base para a imagem da matriz

1 4 1 2 6 0 4 8 - 4

(a) { ( 1 ,   2 ,   4 ) ,   ( 1 ,   0 ,   - 4 ) }

(b) { ( 1 ,   0 ,   0 ) ,   ( 4 ,   2 ,   0 ) }

(c) { ( 1 ,   2 ,   4 ) ,   ( 0 ,   1 ,   4 ) }

(d) { ( 4 ,   6 ,   8 ) ,   ( 1 ,   0 ,   - 4 ) }

Ver solução completa

Questão 17

Considere os vetores v → = 10,11,12 ⊥ ,   w → = 452 , - 113 ⊥ e a matriz A = 1 4 2 5 3 6 . Verifique as afirmativas abaixo:

I - w → ∈ N ( A )

I I - v → ∈ I m ( A )

a )   I é falsa e I I é verdadeira

b)   Ambas são verdadeiras

c) Ambas são falsas

d)   I é verdadeira e I I é falsa

Ver solução completa

Questão 18

Seja A   uma matriz m × n qualquer e b → um vetor qualquer de R m . Verifique as afirmativas abaixo:

I - O núcleo de A é o conjunto-solução do sistema linear A x → = 0 →

II - A imagem de A é o conjunto-solução do sistema linear A x → = b →

(a) I é verdadeira e II é falsa

(b) I é falsa e II é verdadeira

(c) Ambas são falsas

(d) Ambas são verdadeiras

.

Ver solução completa

Questão 19

Sejam A uma matriz quadrada e S o sistema A x → = b → .

( I ) Se quando   S tem solução, a solução é única, então S pode não ter solução para algum b → .

( I I ) Se S tem solução qualquer que seja b → , então S sempre tem solução única.

(a) A afirmativa ( I ) é verdadeira e ( I I ) é verdadeira.

(b) A afirmativa ( I ) é falsa e ( I I )   é verdadeira.

(c) A afirmativa ( I ) é falsa e ( I I ) é falsa.

(d) A afirmativa ( I ) é verdadeira e ( I I ) é falsa.

Ver solução completa

Questão 20

Assinale a matriz cuja imagem é um plano e cujo núcleo é uma reta.

(a) 1 - 1 1 1 - 1 1

(b) 1 - 1 1 1 - 1 1 1 - 1 1

(c) 1 1 2 1 2 3 1 1 2

(d) 1 1 1 1 2 1 1 1 3

Ver solução completa

Questão 21

Seja A x = b um sistema linear m × n qualquer. Considere as seguintes afirmações:

I Se a dimensão do núcleo de A for diferente de zero então A x = b pode ter solução única.

I I Se a dimensão do espaço gerado pelas colunas de A é menor do que m , então pode haver A x = b sem solução.

Qual das opções abaixo é CORRETA?

( a ) A afirmativa I é falsa e I I é falsa.

( b ) A afirmativa I é falsa e I I é verdadeira.

( c ) A afirmativa I é verdadeira e I I é falsa.

( d ) A afirmativa I é verdadeira e I I é verdadeira.

Ver solução completa

Questão 22

Seja A uma matriz m × n e sejam B e C matrizes invertíveis n × n . Dentre as afirmações abaixo, a única falsa (isto é, que não é verdadeira para determinadas escolhas de A , B e C ) é:

a   B C - 1 T = B - 1 T C - 1 T

b I m A B ⊂ I m A (onde I m denota “imagem”)

c   N A B ⊃ N B (onde N denota “núcleo”)

d   B C = C B

Ver solução completa

Questão 23

Qual das matrizes abaixo possui imagem contida no plano x + y + z = 0

( a ) 1 - 2 1 2 1 - 3 1 2 - 3

( b ) 1 2 3 1 2 3 1 2 3

( c ) 1 2 1 - 2 1 2 1 - 3 - 3

( d ) 1 2 1 - 2 1 2 2 - 2 - 2

Ver solução completa

Questão 24

Os valores de a , b , c de forma que o sistema linear 1 2 3 4 5 6 7 8 9 x y z = a b c tenha pelo menos uma solução satisfazem a equação:

a   a - b + 2 c = 0

b   2 a - b + c = 0

( c ) a - 2 b + c ≠ 0

( d ) a - 2 b + c = 0

Ver solução completa

Questão 25

Considere o sistema A x → = b → :

  1. Se não existe solução, então A não é sobrejetiva.
  2. Se tem várias soluções então A pode ser injetiva.

a   I é verdadeira, mas II é falsa.

b   I é falsa, mas II é verdadeira.

c   I e II são verdadeiras.

d   I e II são falsas.

Ver solução completa

Questão 26

Seja

A = 1 2 - 1 1 1 - 1 - 1 - 2 1 2 - 1 1 1 1 - 1 0

Determine qual dos conjuntos abaixo forma uma base para a imagem de A .

( a ) 1,2 , - 1,1 , 1 , - 1 , - 1 , - 2 , 1 , - 1 , - 1,0

( b ) 1,1 , 1,1 , 2 , - 1,2 , 1 , 1 , - 2,1 , 0

( c ) 1,1 , 1,1 , 2 , - 1,2 , 1

( d ) 1,1 , 1,1 , 2 , - 1,2 , 1 , - 1 , - 1 , - 1 , - 1 , 1 , - 2,1 , 0

Ver solução completa

Questão 27

Considere o sistema linear A x = b . Diga se as afirmativas abaixo são verdadeiras ou falsas.

I   Se b pertence ao espaço gerado pelas colunas de A , então A x = b tem solução única.

I I Se b não pertence ao espaço gerado pelas colunas de A , então A x = b tem infinitas soluções.

( a ) Ambas são falsas.

( b ) I é verdadeira e I I é falsa.

( c ) Ambas são verdadeiras.

( d ) I I é verdadeira e I é falsa.

Ver solução completa

Questão 28

Considere os sistemas S : A x → = b → e H : A x → = 0 → e assinale a alternativa INCORRETA:

a   H sempre tem solução

b   Se b ∈ I m A , então S tem solução

c   Se H tem duas soluções, então H tem infinitas soluções

d   Se H tem solução única, então S tem solução única

Ver solução completa

Questão 29

Considere o sistema linear A x = b . Diga se as afirmativas abaixo são verdadeiras ou falsas.

I   Se as colunas de A são linearmente independentes e b pertence à imagem de A , então A x = b tem solução única.

I I Se as colunas de A são linearmente dependentes e b pertence à imagem de A , então A x = b tem infinitas soluções.

Qual das opções abaixo é CORRETA?

( a ) Ambas são falsas.

( b ) Ambas são verdadeiras.

( c ) I é verdadeira e I I é falsa.

( d ) I é falsa e I I é verdadeira.

Ver solução completa

Questão 30

A dimensão da imagem de

É:

(a) 0

(b) 1

(c) 2

(d) 3

Ver solução completa

Questão 31

Assinale a matriz abaixo cujo núcleo é a reta x - y = 0 e cuja imagem é a reta x + y = 0 :

( a ) 1 - 1 - 1 - 1

( b ) 10 10 - 10 - 10

( c ) - 20 - 20 20 20

( d ) - 30 30 30 - 30

Ver solução completa

Questão 32

Qual conjunto abaixo pode ser uma base para a imagem de uma matriz A 3 × 5 ?

( a ) Um conjunto de 5 vetores em R 5

( b ) Um conjunto de 5 vetores em R 3

( c ) Um conjunto de 3 vetores em R 5

( d ) Um conjunto de 3 vetores em R 3

Ver solução completa

Questão 33

Suponha que A = 1 0 2 2 1 1 0 4 0 1 - 2 3 . Então, a dimensão da imagem de A será igual a:

( a ) 0

( b ) 1

c 2

( d ) 3

Ver solução completa

Questão 34

Considere um sistema linear A x = b , onde A é uma matriz quadrada. Considere as afirmações abaixo e assinale a resposta CORRETA:

  1. Se o núcleo de A é uma reta, então o sistema sempre tem solução.
  2. Se A é injetiva, então o sistema pode não ter solução.

a   Ambas são verdadeiras

b   Ambas são falsas

c   I é verdadeira e I I é falsa

d   I é falsa e I I é verdadeira

Ver solução completa

Questão 35

Seja A uma matriz 2 × 5 . Considere as afirmações:

(I) Necessariamente, dim ⁡ N ( A ) > dim ⁡ I m ( A ) .

(II) dim ⁡ I m A T pode ser 3.

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Ver solução completa

Questão 36

Dada uma matriz A, seja L uma matriz obtida reordenando-se as linhas de A e seja C uma matriz obtida reordenando-se as colunas de A.

(I) Se A x → = b → tem solução, então L x → = b → também tem solução.

(II) Se A x → = b → tem solução única, então C x → = b → também tem solução única.

(a) I é falsa e II é falsa.

(b) I é verdadeira e II é falsa.

(c) I é falsa e II é verdadeira.

(d) I é verdadeira e II é verdadeira.

Ver solução completa

Questão 37

O conjunto v → 1 ,   v → 2 , v → 3 é linearmente dependente e o conjunto v → 2 , v → 3 , v → 4 é linearmente independente. Seja A a matriz cujas colunas são os vetores v → 1 ,   v → 2 , v → 3 . Assinale a resposta CORRETA:

( a ) O sistema A X → = v → 4 não possui solução.

( b ) O sistema A X → = v → 1 possui solução única.

( c ) O sistema A X → = v → 2 não possui solução.

( d ) O sistema A X → = v → 3 possui solução única.

Ver solução completa

Questão 38

Considere os sistemas equivalentes A x = b 1 e B x = b 2 , onde B b 2 é a matriz obtida de A b 1 após o escalonamento. Assinale a afirmativa FALSA:

( a ) O conjunto solução de A x = b 1 é igual ao de B x = b 2

( b ) O conjunto solução de A x = 0 é igual ao de B x = 0 .

( c ) O espaço gerado pelas linhas de A é igual ao espaço gerado pelas linhas de B .

( d ) O espaço gerado pelas colunas de A é igual ao espaço gerado pelas colunas de B .

Ver solução completa

Questão 39

Qual das matrizes abaixo possui imagem contida no plano x + y + z = 0 ?

( a ) 1 - 1 1 1 1 - 1 - 1 1 1

( b ) 1 2 3 1 2 3 1 2 3

( c ) 1 1 - 2 - 1 1 0 1 - 1 0

( d ) 1 - 1 1 1 1 - 1 - 2 0 0

Ver solução completa

Questão 40

Seja n um inteiro positivo e sejam A , B ∈ M n R tais que a matriz B seja obtida da matriz A por operações elementares de escalonamento em linhas. Assinale a alternativa contendo uma afirmação que NÃO é necessariamente verdadeira:

  1. os sistemas lineares homogêneos A X   =   0 e B X   =   0 (na incógnita X ∈ M n × 1 R ) possuem as mesmas soluções;
  2. det ( A )   =   det ( B ) ;
  3. se o sistema linear homogêneo A X   =   0 (na incógnita X ∈ M n × 1 R ) possui infinitas soluções, então det ( B )   =   0 ;
  4. qualquer linha de A é uma combinação linear das linhas de B ;
  5. se as linhas da matriz B são linearmente independentes, então o sistema linear A X   =   Y (na incógnita X ∈ M n × 1 R ) possui uma única solução, para qualquer Y ∈ M n × 1 R .

Ver solução completa

Questão 41

Seja A uma matriz quadrada, n × n . Considere as afirmativas abaixo:

  1. Se A é injetiva, então o sistema A x → = b → sempre tem mais de uma solução.
  2. Se A é sobrejetiva, então o sistema A x → = b → sempre tem solução única.

a   Ambas são falsas

b   Ambas são verdadeiras

c   I é falsa e I I é verdadeira

d   I é verdadeira e I I é falsa

Ver solução completa

Questão 42

Qual das matrizes abaixo possui imagem contida no plano x + y + z = 0 ?

a   1 1 1 - 1 1 1 1 - 1 - 1

b   1 2 3 1 2 3 1 2 3

c   1 - 1 0 1 1 - 2 1 1 - 2

d   1 1 1 - 1 1 1 0 - 2 - 2

Ver solução completa

Listas de Exercícios Resolvidos

Lista de Introdução às EDO'sLista de Subespaços VetoriaisLista de ElipsesLista de Parábolas Lista de Combinação LinearLista de Ângulos entre RetasLista de Posições Relativas de RetasLista de Reflexão OrtogonalLista de Expressão Analítica de uma TLLista de Complemento Ortogonal e Soma Direta

Principais Conceitos de Álgebra Linear e Geometria Analítica

Equação da Esfera