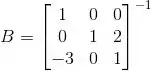Exercícios de Matriz Inversa - Lista de Exercícios Resolvida

Calcule a terceira coluna da inversa da matriz:

Considera a matriz quadrada de ordem :

Onde é um número real.

Podemos afirmar que:

a) não é invertível para nenhum valor de

b) é invertível para um único valor de

c) é invertível para exatamente dois valores de

d) é invertível para todos os valores de

A matriz possui inversa . Determine e tais que:

Sendo

Inverta:

Se são invertíveis e , então

Considera a matriz dada:

Onde e são números reais. Se e é invertível, então:

a) e

b) e

c) e

d) e

Considere as afirmativas abaixo:

I – Uma matriz é invertível somente se para o sistema a solução for sempre .

II – A inversa da matriz identidade é

III – A matriz é invertível e a sua inversa é triangular superior.

Estão corretas, apenas:

a) I e II

b) I

c) II e III

d) III

e) I, II e III

f) II

g) I e III

Se a inversa de é , qual o valor de ?

Calcule as inversas das seguintes matrizes:

(b)

19) Considere a matriz

Onde . Mostre que é invertível e encontre a sua inversa.

Calcule as inversas das seguintes matrizes:

(a)

Calcule as inversas das seguintes matrizes:

(c)

Encontre a inversa de

21) A soma de matrizes invertíveis é invertível?

22) Sejam e matrizes quadradas tais que . Mostre que se é invertível, então .

28) Encontre a inversa das matrizes:

28) Encontre a inversa das matrizes:

28) Encontre a inversa das matrizes:

Encontre a inversa das matrizes:

Encontre a inversa das matrizes:

Mostre que é não-invertível para quaisquer valores das entradas.

Encontre a inversa das matrizes:

Resolva o sistema invertendo a matriz dos coeficientes:

(c)

Resolva o sistema invertendo a matriz dos coeficientes:

(a)

Resolva o sistema invertendo a matriz dos coeficientes:

(d)

Resolva o sistema invertendo a matriz dos coeficientes:

(b)

33) Seja um sistema homogêneo de equações lineares e incógnitas cuja única equação é a trivial. Mostre que se é um qualquer inteiro positivo, então o sistema também só tem a solução trivial.

37) Encontre todos os valores de e para os quais e são ambas não invertíveis.

Seja .

Qual das matrizes poderia ser a inversa de ?

Das matrizes abaixo, assinale a que é invertível.

Seja

Qual das matrizes poderia ser a inversa de ?

Seja a transformação linear que satisfaz e . A matriz que representa é:

1. .
2. .
3. .
4. .

Considere as afirmativas:

1. Sejam e matrizes invertíveis. Se e comutam (isto é, ) então e comutam.
2. Seja uma matriz invertível. Então .

1. (I) é falsa e (II) é falsa.
2. (I) é verdadeira e (II) é falsa.
3. (I) é falsa e (II) é verdadeira.
4. (I) é verdadeira e (II) é verdadeira.

Seja

Qual das matrizes poderia ser a inversa de ?

a) Determine a matriz inversa de

Considere o produto , onde e são matrizes que representam transformações bijetivas:

As linhas de são combinações lineares das linhas de

As linhas de são combinações lineares das linhas de

a) é verdadeira e é falsa

b) é falsa e é verdadeira

c) Ambas são verdadeiras

d) Ambas são falsas

Calcule a matriz inversa da matriz e assinale a soma dos elementos de sua primeira coluna:

a)

b)

c) 0

d)

Seja , a inversa de é da forma:

(a)

(b)

(c)

(d)

Considere as matrizes e .

(b) Determine a inversa de B, a matriz

Considere a matriz

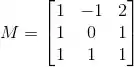
e a transformação linear cuja matriz na base canônica é M.

(a) Determine a matriz inversa de M.

Seja A uma matriz na forma

Onde cada representa um número diferente de zero. (Dois quadradinhos idênticos podem representar números diferentes). Então a inversa de A tem a forma:

(a)

(b)

(c)

(d)

A terceira coluna da inversa da matriz é

Sejam e as matrizes abaixo, determine o elemento da segunda linha e da segunda coluna da matriz .

Seja

Então vale:

1. .
2. .
3. .
4. .

28) Encontre a inversa das matrizes:

Encontre a inversa das matrizes:

Determine se as afirmações abaixo são verdadeiras ou falsas. Justificando sua resposta.

(b) Se e são matrizes semelhantes, então .

Seja e considere a matriz dada por

A soma dos elementos na diagonal principal da matriz é igual a

a)

b)

c)

d)

e)

Calcule a terceira coluna da inversa da matriz:

A soma das entradas de B é:

(a) -6

(b) -2

(c) 4

(d) 8

Seja . Qual das matrizes poderia ser a inversa de ?

13 – Considere as matrizes:

Sabendo-se que

E que a matriz é diagonal, temos que a soma das duas entradas na primeira coluna da matriz é igual a:

a)

b)

c)

d)

e)

Considere a matriz

Tal matriz é inversível? Em caso afirmativo, determine .

Considere a matriz

calcule , a entrada vale:

Seja

Então,

(a) A é invertível para todo (a, b, c)

(b) A não é invertível para todo (a, b, c)

(c) A só é invertível para todo (a, b, c) (1, 1, 1)

(d) A só é invertível se (a, b, c) é um múltiplo de (1, 1, 1)

Determine a inversa da matriz

Determine a inversa da matriz

Observe bem as matrizes abaixo e assinale aquela que é invertível:

Suponha que as operações matriciais indicadas estão definidas.

(a) Vale a relação ?

A inversa da matriz é dada por

Seja . A solução do sistema é:

Considere a matriz:

Temos que a soma das entradas na diagonal principal da matriz é igual a:

1. ;
2. ;
3. ;
4. ;
5. .

Encontre a inversa de

28) Encontre a inversa das matrizes:

Seja .

Qual das matrizes poderia ser a inversa de ?

Assinale a matriz que pode ser a inversa da matriz