Exercícios de Resolvendo Sistemas Lineares - Lista de Exercícios Resolvida
Questão 1
Mostre que o conjunto solução do sistema :
não irá se alterar se acrescentarmos a equação ___ (não resolva o sistema!)
Ver solução completaQuestão 3
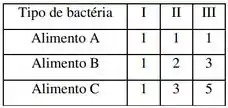
Um biólogo colocou três espécies de bactérias (denotadas por I, II e III) num tubo de ensaio, onde elas serão alimentadas por três fontes diferentes de alimentos (A, B e C). Em cada dia serão colocadas no tubo de ensaio 1500 unidades de A, 3000 unidades de B e 4500 unidades de C. Cada bactéria consome um certo número de unidades de cada alimento por dia, como mostra a tabela. Quantas bactérias podem coexistir no tubo de ensaio de modo a consumir todo o alimento?
Questão 5
Se o termo é a solução do sistema abaixo, então é igual a:
a) -8
b) -7
c) -6
d) -5
e) -4
Ver solução completaQuestão 6
Resolva o sistema abaixo pelos métodos pedidos.
a) Método da substituição.
b) Método da adição.
c) Escalonamento.
Ver solução completaQuestão 7
Resolva o sistema linear abaixo, escrevendo o conjunto-solução em equações paramétricas:
Ver solução completaQuestão 8
Considere o sistema linear
- Encontre todas as soluções do sistema homogêneo associado e represente este espaço de soluções como um espaço gerado.
- Verifique que é solução do sistema não-homogêneo acima.
- Enconte todas as soluções e represente-as como um espaço gerado deslocado da origem.
Questão 10
Assinale a solução geral do sistema linear representado pela matriz aumentada:
Ver solução completa
Questão 11
Considere o sistema onde e
A soma das entradas da única solução do sistema vale:
Ver solução completa
Questão 14
Encontre as matrizes , e que expressem o sistema de equações lineares dado como uma única equação matricial .
(a)
Ver solução completaQuestão 15
Encontre as matrizes , e que expressem o sistema de equações lineares dado como uma única equação matricial .
(b)
Ver solução completaQuestão 16
Nos itens abaixo, suponha que a matriz aumentada de um sistema de equações lineares foi reduzida por operações sobre linhas à forma escalonada. Resolva o sistema.
b)
Ver solução completaQuestão 17
Nos itens abaixo, suponha que a matriz aumentada de um sistema de equações lineares foi reduzida por operações sobre linhas à forma escalonada. Resolva o sistema.
a)
Ver solução completaQuestão 18
Resolva os seguintes sistemas homogêneos de equações lineares por qualquer método:
a)
Ver solução completaQuestão 19
Nos itens abaixo, suponha que a matriz aumentada de um sistema de equações lineares foi reduzida por operações sobre linhas à forma escalonada. Resolva o sistema.
c)
Ver solução completaQuestão 20
Resolva os seguintes sistemas homogêneos de equações lineares por qualquer método:
b)
Ver solução completaQuestão 21
Nos itens abaixo, suponha que a matriz aumentada de um sistema de equações lineares foi reduzida por operações sobre linhas à forma escalonada. Resolva o sistema.
d)
Ver solução completaQuestão 23
Qual das expressões abaixo NÃO REPRESENTA a solução geral do sistema:
Ver solução completa
Questão 24
Considere o sistema linear de equações
- Determine e para que o sistema tenha infinitas soluções.
- Determine e para que o sistema não tenha solução.
- Ache a solução do sistema quando e .
Questão 25
Considere a seguinte matriz ampliada de um sistema de equações lineares. Quais as condições que e devem satisfazer pra que o sistema tenha infinitas soluções? Neste caso, qual o grau de liberdade do sistema?
Ver solução completaQuestão 26
Qual é a solução geral do sistema abaixo?
Obs: abaixo, s e t são parâmetros reais.
(a)
(b)
(c)
(d)
Ver solução completaQuestão 27
Considere o sistema abaixo e assinale o valor de quando
(a)
(b)
(c)
(d)
Ver solução completaQuestão 28
Considere o sistema abaixo e assinale o conjunto que NÃO REPRESENTA a sua solução geral:
(a)
(b)
(c)
(d)
Ver solução completaQuestão 29
A última equação do sistema linear abaixo é uma combinação das três primeiras. A soma dos coeficientes dessa combinação é:
(a) 3
(b) −1
(c) 0
(d) 2
Ver solução completaQuestão 30
Se é solução do sistema
então x + z é igual a:
(a) 11
(b) 9
(c) 5
(d) 7
Ver solução completaQuestão 31
Sejam e considere o sistema linear
nas incógnitas reais Considere também as seguintes afirmações:
(I) se são tais que esse sistema possui solução, então o seu conjunto solução será descrito usando no máximo uma variável livre;
(II) esse sistema é impossível para certos valores de ;
(III) se esse sistema tiver infinitas soluções, então .
As afirmações verdadeiras são:
- apenas a 2
- apenas a 1 e 2
- apenas a 1
- apenas a 2 e 3
- apenas a 1 e 3
Questão 32
O sistema linear associado à matriz aumentada:

Tem solução única Então é:
(a) 8
(b) 18
(c) 22
(d) 26
Ver solução completaQuestão 33
Podemos afirmar que a solução do sistema linear
É uma reta que passa pela origem.
É um plano que não passa pela origem.
É um plano que passa pela origem.
É uma reta que não passa pela origem.
Ver solução completaQuestão 34
A soma dos componentes do vetor solução do sistema linear representado pela matriz aumentada é:
Ver solução completa
Questão 35
Dada uma matriz , podem existir vetores não nulos , tais que , onde (nesse caso é dito autovetor de associado ao escalar ).
Suponha que e . Então, se sabemos que a primeira coordenada de é igual a , a soma das coordenadas de será igual a:
Ver solução completa
Questão 37
Assinale, dentre os sistemas abaixo, aquele cujo conjunto-solução é o plano gerado pelos vetores e :
Ver solução completa
Questão 38
Sejam , matrizes e uma matriz .
Se a matriz existe e
admite solução? A solução é única? Justifique sua resposta.
Ver solução completaQuestão 39
Sejam e os seguintes sistemas lineares representados pelas suas matrizes aumentadas:
Considere as afirmações abaixo e assinale a resposta correta:
- Se o sistema tem apenas a solução trivial, então o sistema não possui solução.
- Se o sistema tem solução, então o sistema tem uma solução não-trivial
Ambas são verdadeiras.
é verdadeira e é falsa.
Ambas são falsas.
é verdadeira e é falsa
Ver solução completaQuestão 40
Quais valores de e fazem com que o sistema linear a seguir não tenha solução?
Ver solução completa
Questão 41
Um dado é lançado vezes seguidas e os obtidos, , e , formam o lado direito do sistema abaixo:
Podemos afirmar que o sistema possui:
Uma chance em de ter solução
Uma chance em de ter solução
Uma chance em de ter solução
Uma chance em de ter solução
Ver solução completaQuestão 42
Considere o seguinte sistema linear:
Assinale os valores de para os quais o sistema tem mais de uma solução:
e
Ver solução completaQuestão 44
Considere o sistema de equações lineares
Onde é um número real.
(a) Obtenha uma forma escalonada para a matriz aumentada do sistema acima.
(b) Com base na matriz obtida no item (a), determine para quais valores de o sistema não admite solução, para quais admite uma única solução, e para quais valores admite infinitas soluções.
(c) Determine as soluções do sistema no caso em que e as escreva na forma vetorial paramétrica.
Ver solução completaQuestão 45
Determine se as afirmações abaixo são verdadeiras ou falsas. Prove as verdadeiras e apresente um contra-exemplo para as falsas.
b) Se e são matrizes , então
Ver solução completaQuestão 46
Considere , onde é , e seja a forma escalonada. Assinale a afirmativa FALSA:
Se então
Se então
Se então
Ver solução completaQuestão 48
Q2. Seja uma matriz real e seja o operador linear tal que , em que can denota a base canônica de . Suponha que o polinômio característico de seja
E que
e ,
Em que denota o autovalor de que tem a parte imaginária positiva e denota o operador identidade de . Temos que a solução geral real do sistema de equações diferenciais é dada por:
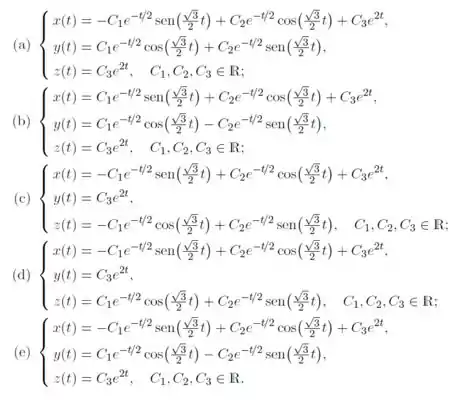
Questão 49
Sobre as soluções de um sistema linear , onde é , assinale a afirmativa VERDADEIRA:
São os coeficientes de uma combinação linear das colunas de
São vetores de
São os coeficientes de uma combinação linear das linhas de
São as colunas de
Ver solução completaQuestão 50
Uma matriz foi escalonada, sofrendo consecutivamente as seguintes operações-linha:
O resultado deste escalonamento é a matriz . Qual é a solução de ?
Ver solução completa
Questão 51
A soma dos componentes do vetor solução do sistema linear representado pela matriz aumentada é:
Ver solução completa
Questão 52
Quais valores de e fazem com que o sistema linear a seguir tenha solução única?
Ver solução completa
Questão 53
Quais das expressões abaixo representa a solução geral da equação linear . (, são parâmetros reais.)
Ver solução completa
Questão 54
O sistema linear representado pela matriz aumentada possui solução única. A soma dos componentes do vetor solução é:
Ver solução completa
Questão 55
Sejam Considere o sistema linear
Assinale a afirmação verdadeira
não existe valor de para que o sistema seja compatível indeterminado
se , o sistema tem exatamente uma variável livre
Se o sistema é compatível e indeterminado então
o sistema é compatível para quaisquer
o sistema é compatível determinado se, e somente se,
Ver solução completaQuestão 57
Classifique as afirmativas abaixo:
- Existem dois números positivos tais que a razão entre a sua diferença e a sua soma é igual à razão entre eles.
- Existem dois números positivos tais que a razão entre a sua soma e a sua diferença é igual à razão entre eles.
- I é falsa e II é verdadeira.
- Ambas são falsas.
- I é verdadeira e II é falsa.
- Ambas são verdadeiras.
Questão 58
Assinale abaixo a soma das componentes de um vetor solução do sistema linear representado pela matriz aumentada:
Ver solução completa
Questão 59
A soma dos componentes do vetor solução do sistema linear representado pela matriz aumentada
É:
Ver solução completa
Questão 61
Assinale o conjunto que representa TODAS as soluções do sistema , onde indica o espaço derado por .
Ver solução completa
Questão 62
Quais são todos os possíveis valores de e para que o sistema linear a seguir não tenha solução?
Ver solução completa
Questão 63
Quais valores de e fazem com que o sistema linear a seguir tenha solução única?
Ver solução completa
Questão 64
Assinale a alternativa FALSA:
(a) Seja uma matriz e o núcleo de um espaço de dimensão . O sistema pode não ter solução.
(b) Seja uma matriz e o núcleo de um espaço de dimensão . O sistema pode não ter solução.
(c) Se e tem o mesmo núcleo então a matriz é quadrada
(d) Se sempre tem pelo menos uma solução então a única solução de é .
(e) Não sei.
Ver solução completaQuestão 65
Assinale abaixo o valor da segunda componente da solução do sistema linear representado pela matriz aumentada
Ver solução completa
Questão 67
Deseja-se encontrar o polinômio da forma cujo gráfico passe pelos pontos e . O vetor de coeficientes :
não pode ser calculado pela solução de um sistema linear, pois trata-se de um problema quadrático.
é solução do sistema linear representado por
é solução do sistema linear representado por
é solução do sistema linear representado por
Ver solução completaQuestão 68
Quais são todos os possíveis valores de e para que o sistema linear a seguir tenha infinitas soluções.
Ver solução completa
Questão 69
A soma dos componentes do vetor solução do sistema linear representado pela matriz aumentada é:
Ver solução completa
Questão 71
Resolva os seguintes sistemas homogêneos de equações lineares por qualquer método:
c)
Ver solução completaQuestão 74
O sistema abaixo possui solução única qualquer que seja o vetor do lado direito.
Assinale o vetor que produz o menor valor para a soma , onde é a solução do sistema acima:
Ver solução completa
Questão 76
Considere o sistema linear representado pela seguinte matriz aumentada:
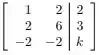
O valor de tal que o sistema tem solução é:
(A)
(B)
(C)
(D)
Ver solução completa