Uma barra delgada de comprimento é envergada até formar um semi-círculo, conforme mostra a Figura 1.
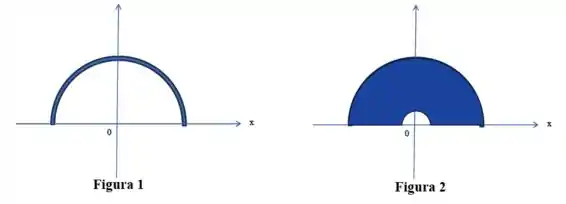
Se a barra tem uma densidade de carga uniforme , calcule o campo elétrico na origem.
Onde deveria ser colocada uma carga pontual de valor igual ao da carga total da barra para que o campo na origem fosse nulo?
Considere agora que esse semicírculo se torne um semi-disco de mesmo raio com um orifício concêntrico semicircular de raio e com uma densidade superficial uniforme , como mostrado na Figura 2. Calcule o campo elétrico na origem devido a esta nova configuração.
Passo 1
Para calcular o campo elétrico na origem, devido a barra carregada, podemos usar a equação do campo gerado por uma carga infinitesimal:
Pela simetria, vemos que dois pontos simétricos em relação ao eixo , produzem campos infinitesimais cujas componentes irão cancelar, sobrando apenas as componentes que estão se somando! Então, queremos:
No nosso caso, temos , substituindo:
Integrando:
Onde , logo:
Passo 2
Para que o campo em seja nulo, o campo gerado pela carga deve ser igual em módulo ao campo gerado pelo fio, e de sinal oposto para poder cancelá-lo. O campo gerado pela carga é dado por:
Como a carga possui a mesma carga total da barra:
Substituindo e igualando ao valor do campo:
A carga , por ter mesmo sinal que a barra, deve ser colocada no lado oposto, ou seja:
Passo 3
Para determinar o campo na origem, devido o disco carregado, podemos partir do que já calculamos no item , para um semicírculo à uma distancia da origem, temos que o campo gerado é:
Integrando de até , temos:
Resposta