Dois fios retilíneos de mesmo comprimento , separados por uma distância , estão uniformemente carregados com densidades lineares de carga e . Considerando o sistema de coordenadas abaixo, calcule:
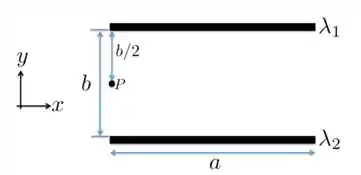
- O vetor campo elétrico no ponto ;
- O potencial elétrico no ponto ;
- O trabalho que um agente externo deve realizar sobre uma carga para trazê-la desde o infinito até o ponto .
Passo 1
a) Para a gente matar essa questão, considere a figura abaixo. O vetor localiza o elemento de carga no fio, enquanto o vetor localiza o ponto onde queremos calcular o campo elétrico resultante. O ponto está sobre o eixo .
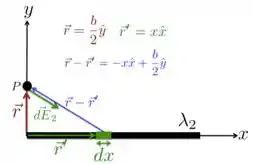
Vamos tomar primeiro a barra com densidade de carga . Olhando para a figura, a gente vê que o elemento de carga está a uma distância do ponto e o campo elétrico produzido por é:
em que ’ é o vetor unitário que está ao longo da reta que une e o ponto . Sempre podemos escrever um vetor unitário da seguinte maneira:
isto é, o vetor dividido pelo módulo dele. Utilizando a representação vetorial que colocamos na figura, podemos reescrever o campo elétrico produzido por como:
que mostra que esse campo tem componentes ao longo do eixo e .
Mas não queremos apenas o campo produzido por esse do fio 2, queremos o campo produzido pelos dois fios no ponto .
Passo 2
a) (Continuação)
Antes de fazer a integral para todo o fio, vamos colocar agora no ponto o campo produzido também por um elemento de carga , mas que agora está no fio 1 à mesma altura do elemento que a gente discutiu no passo anterior. O campo produzido por esse do fio 1 é no sentido de se afastar do fio, pois a carga do fio 1 é positiva. Isso está na figura abaixo.
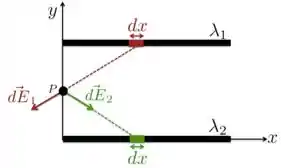
Vemos que esse campo pode ser obtido de maneira similar ao que fizemos para . Como esse elemento do fio 1 está à mesma distância do eixo , o campo que ele produz é:
cujas componentes podemos conferir a partir da figura acima. Portanto, o campo elétrico resultante sobre o ponto devido às cargas e dos fios 1 e 2, respectivamente, é:
Agora sim, vamos integrar essa expressão para obter o campo resultante no ponto produzido pelos fios 1 e 2. Fazendo isso, temos:
Utilizando o resultado
Vamos ter
Finalmente chegamos a:
que mostra que o campo elétrico resultante produzido pelos dois fios carregados aponta do eixo e não tem componente ao longo da direção do eixo .
Passo 3
b) Na última figura acima, vemos que os elementos de cargas, que têm o mesmo módulo mas sinais contrários, estão à mesma distância do ponto . Portanto, se somamos as contribuições de cada elemento de carga desse para o potencial, obteremos um valor NULO no ponto .
A gente pode repetir essa ideia para toda a extensão restante dos dois fios e obteremos que o potencial no ponto devido aos dois fios é NULO. Ou seja, sempre há uma carga no fio 1 produzindo um potencial que é cancelado pelo potencial de uma carga do fio 2 com mesmo módulo e à mesma distância do ponto .
Por isso, o potencial total em devido aos fios é NULO: .
Passo 4
c) O trabalho realizado pelo campo para trazer uma partícula carregada do infinito ao ponto é:
em que é o trabalho realizado por um agente para trazer do infinito para .
Bom, como vimos, o potencial no ponto é . O potencial no infinito também é zero: . Portanto, a partir da expressão acima, chegamos a: