Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Elétrico Gerado por uma Linha de Cargas

Ver Teoria
Exercício 4712345678910111213141516171819202122232425262728293031323334353637383940414243444546484950515253545556575859606162636465666768697071727374757677787980818283848586

Enunciado

Puc - Física 3 – P1 2018.2 - 2

Parte I ) Considere uma esfera isolante, que está mostrada na figura abaixo, de raio R e densidade volumétrica de carga ρ r = Q π r R 4 , onde Q é a carga total da esfera isolante. Utilizando a lei de Gauss,

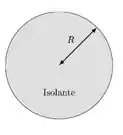
  1. Determine o campo elétrico na região r < R .
  2. Determine do campo elétrico na região r > R .

    3. Parte I I ) Uma esfera isolante de raio R foi envolta por uma casca esférica condutora de carga líquida nula. Essa casca esférica, em equilíbrio eletrostático, possui raio interno R e raio externo 2 R , como mostra a figura abaixo. Nesta situação, considere que a carga total da esfera isolante é Q , distribuída uniformemente no seu interior.

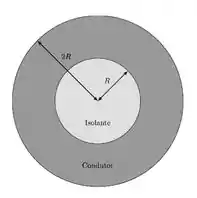
  3. Determine o campo elétrico na região R < r < 2 R .
  4. Determine o campo elétrico na região r > 2 R .

Passo 1

a) Como a distribuição de cargas depende apenas da distância radial r , temos simetria esférica. Isso significa que se fizermos uma rotação da esfera de qualquer ângulo em torno de qualquer reta passando pelo seu diâmetro, a distribuição de cargas permanece a mesma. Essa simetria faz com que o campo elétrico gerado por essa distribuição tenha propriedades específicas.

A primeira delas é que o módulo deste campo depende apenas da distância radial r e a outra é que ele está orientado ao longo da direção radial  r ^ :

E → = E r r ^   .

Depois disso, por causa dessa simetria, devemos escolher como nossa gaussiana uma esfera, neste caso uma esfera concêntrica à esfera isolante com raio r < R .

Vamos aplicar a lei de Gauss. Para isso, tomamos a figura abaixo como nossa referência: o elemento  d A → apontando para fora da gaussiana. Como o problema não disse se a carga é positiva ou negativa, vamos colocar como positiva para que  E → seja paralelo a  d A → .

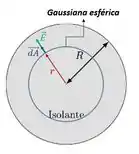
Como E ( r ) tem o mesmo valor em todos os pontos da gaussiana, então teremos na lei de Gauss o seguinte:

Φ E = ∮ G E → ⋅ d A → = E r ∮ G d A = E ( r ) ( 4 π r 2 ) = Q i n t e ε 0   .

Agora, precisamos ver quanto de carga há na região r < R . Para isso, temos que fazer a seguinte integral:

Q i n t e = ∫ 0 r ρ r d V = Q π R 4 ∫ 0 r 4 π r ' 3 d r ' = Q r 4 R 4   .

Jogando na lei de Gauss, teremos

E r 4 π r 2 = Q r 4 ε 0 R 4 ⇒ E r = 1 4 π ε 0 Q r 2 R 4   .  

Portanto, para r < R , o vetor campo elétrico é

E → = 1 4 π ε 0 Q r 2 R 4   r ^   .

Passo 2

b) Para a região em que r > R , o lado esquerdo da lei de Gauss permanece o mesmo, e o lado direito será apenas a carga total Q da esfera. Por isso, teremos

E r 4 π r 2 = Q ε 0     ⇒     E → = 1 4 π ε 0 Q r 2   r ^   .

Passo 3

c) Como na região em que R < r < 2 R temos um condutor em equilíbrio eletrostático, o campo elétrico nessa região deve ser nulo:   E → = 0 .

Passo 4

d) Para r > 2 R , temos que fazer uma gaussiana concêntrica ao condutor e ao isolante. Nesse caso, como o condutor tem carga líquida nula e o isolante tem carga total Q , então, pela lei de Gauss, teremos

E r 4 π r 2 = Q i n t e ε 0 = Q ε 0     ⇒   E → = 1 4 π ε 0 Q r 2   r ^   .  

Resposta

  1. E → = 1 4 π ε 0 Q r 2 R 4   r ^   ;
  2. E → = 1 4 π ε 0 Q r 2   r ^   ;
  3. E → = 0   ;
  4. E → = 1 4 π ε 0 Q r 2   r ^   .

Exercícios de Livros Relacionados

Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitos anéis circulares de carga.
Se E é a magnitude do campo num ponto P situado a uma distância D de um plano uniformemente carregado com densidade superficial de carga σ . A maior contribuição para E provém dos pontos mais próximos
Duas lâminas carregadas, infinitas e não condutora, são paralelas entre si, estando a lâmina A no plano x = - 2,0m e lâmina B no plano x = + 2,0m . Determine o campo elétrico na região x- 2,0m , na re
Uma linha uniformemente carregada, com densidade linear de carga λ à 3,5n C / m 2 , está no eixo x entre x = 0 e x = 5,0m . (a) Qual é a carga total? Determine o campo elétrico no eixo x em (b) x = 6,
Uma carga positiva está distribuída uniformemente ao longo de todo o comprimento do eixo x e uma carga negativa está distribuída uniformemente ao longo de todo o eixo y . A carga por unidade de compri