Campo Elétrico, Densidade de Carga, Campos Elétricos e Corpos Carregados
Um fio de comprimento está alinhado com o eixo e carregado uniformemente com uma densidade linear de carga . Determine uma expressão para o vetor campo elétrico em um ponto arbitrário do eixo , conforme mostra a Figura 1.
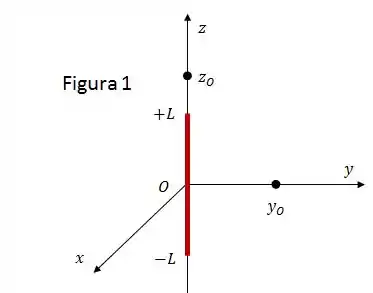
Determine agora uma expressão para o vetor campo elétrico em um ponto arbitrário do eixo , para o mesmo fio do item e da Figura 1.
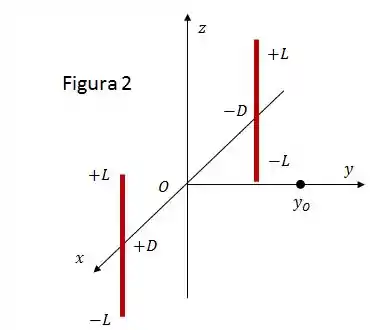
Considere agora dois fios de lados paralelos ao eixo , simetricamente dispostos em relação ao mesmo, afastados entre si da distância e carregados uniformemente com a densidade linear de carga , conforme mostra a Figura 2.
Utilize, adaptando-a, a solução do item para determinar o vetor campo elétrico devido aos fios num ponto arbitrário do eixo .
Passo 1
Um fio de comprimento está alinhado com o eixo e carregado uniformemente com uma densidade linear de carga . Determine uma expressão para o vetor campo elétrico em um ponto arbitrário do eixo , conforme mostra a Figura 1.
Vamos começar considerando o campo elétrico gerado por um pedaço infinitesimal do fio de carga , de forma que:
Assim, o campo elétrico será dado por:
Graficamente, o que acontece é o seguinte:
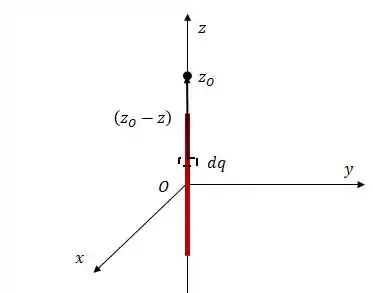
Onde:
Portanto, substituindo isso na expressão que nós encontramos pra , teremos:
Pra terminar, só precisamos integrar esse cara de até :
Passo 2
Resolvendo a integral, teremos:
Substituindo os limites de integração:
Passo 3
Determine agora uma expressão para o vetor campo elétrico em um ponto arbitrário do eixo , para o mesmo fio do item e da Figura 1.
Beleza! A ideia aqui é a mesma de antes... nós começamos escrevendo o campo elétrico gerado por uma carga . Da mesma forma que antes, teremos:
A diferença agora é na direção e sentido desse campo elétrico... dá uma olhada como isso aqui fica graficamente agora:
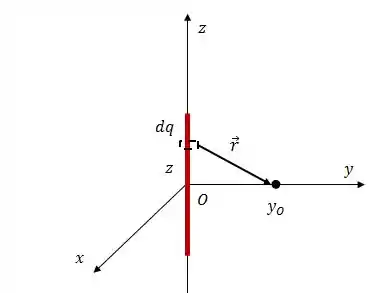
Onde:
Substituindo na expressão de , teremos:
Finalmente, integrando esse cara:
Passo 4
Podemos dar uma organizada nisso separando as integrais pelos vetores unitários:
Sim, eu sei... esse é aquele momento que você bota a mão na cabeça e pensa que está tudo perdido... e geralmente esse momento coincide com aquele em que a sua mãe, ou familiar próximo, entra no seu quarto ou te liga só pra perguntar quanto tempo falta pra você se formar...
Mas não tema!
Essas integrais costumam aparecer bastante nesse tipo de problema... e como o foco aqui não é saber se você consegue resolver essas integrais, a resposta delas geralmente está no formulário da sua prova... então na hora da prova, dá uma olhada e vê se bate com o que você está resolvendo. Você só precisa prestar bastante atenção aos detalhes na hora de comparar o que está na sua folha de prova com o formulário.
Bom, a resposta aqui é a seguinte:
Substituindo os valores, teremos:
Agora é só dar uma organizada aqui:
Passo 5
Considere agora dois fios de lados paralelos ao eixo , simetricamente dispostos em relação ao mesmo, afastados entre si da distância e carregados uniformemente com a densidade linear de carga , conforme mostra a Figura 2.
O campo elétrico resultando no ponto será a resultante da soma vetorial dos campos gerados pelos dois fios.
Olhando de cima, o que teremos é o seguinte:
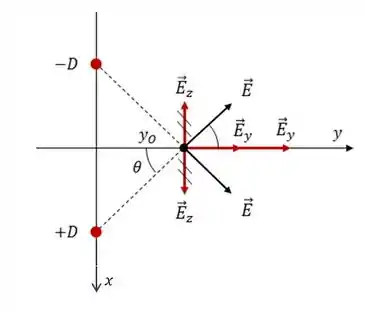
Pela figura acima, dá pra ver que as componentes na direção vão se anular. Assim, o campo elétrico resultante será:
Onde:
O campo elétrico gerado pelo fio no ponto , adaptando a resposta da letra (onde a distância do fio ao ponto será, e não mais , como era antes) será:
Basicamente, o que fizemos aqui foi o seguinte... onde tinha na fórmula da letra , nós colocamos , que é a nova distância do fio ao ponto , entendeu?
Substituindo e na expressão de , teremos:
Simplificando tudo isso:
Resposta