Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Elétrico Gerado por uma Linha de Cargas

Ver Teoria
Exercício 2512345678910111213141516171819202122232426272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586

Enunciado

USP - Física 3 - Provas antigas - Prova substitutiva- 2022.1 - 2

Em um fio muito longo de raio R, centrado ao longo do eixo z, passa uma corrente I (no sentido de z positivo). A corrente elétrica está distribuída no fio de tal forma que a densidade de corrente J → é dada por J → r = K r 2 k ^ na região 0 ≤ r ≤ R, onde K é uma constante positiva.

(a) (0,5 ponto) Determine a dimensão da constante K no sistema internacional de unidades.

(b) (1,0 ponto) Determine a corrente total I que passa pelo fi o. Expresse sua resposta em termos de K e R.

(c) (1,0 ponto) Encontre o vetor campo magnético B → nas regiões 0 ≤ r ≤ R e r > R.

Expresse sua resposta em termos de K, R, e r.

Passo 1

Salve gente bonita!!! Vamos lá resolver essa questão. Primeiro a questão nos entrega que existe um fio muito longo de raio R e que nele é passado uma corrente I no sentido z positivo. Você sabe como o campo se manifesta nessa forma? Vamos já calcular! Temos então que, para o item:

  1. Para descobrirmos a resposta desse item, vamos adotar a formula que a questão nos entrega:

    2. J → r = K r 2 k ^

    Para isolar a constante K na equação que nos é fornecida na questão e depois substituir as variáveis por suas grandezas

    Normalmente se substitui pelos seus valores, mas como queremos saber a dimensão, vamos trocá-las pelas grandezas.

    Assim, temos

    J r = K r 2

    K = J ( r ) r 2

    Substituindo:

    K = A / m 2 m 2

    K = A m 4

    Passo 2

  2. Pessoal, para determinar a corrente vocês tem alguma ideia? Eu sugiro que vamos partir da integral que envolve a densidade de corrente e a área em questão, a partir de uma lei de Maxwell que explanei na formula abaixo. Daí, vamos resolver a integral e substituir o que for necessário para que fique em função das variáveis desejadas. Sacou? Bora lá.

    3. Assim, temos

    I = ∫ J → r . d A →

    Ressalto que d A → será substituído por 2 π r d r k ^ , pois a área é como se fosse a sobreposição de vários círculos que variam de acordo com o raio.

    Assim,

    I = ∫ J → r . d A →

    I = ∫ 0 R ( K r 2 k ^ ) . ( 2 π r d r k ^ )

    Tirando da integral o que não está variando, temos:

    I = 2 π K ∫ 0 R r 3 d r

    I = 2 π K R 4 4

    I = π K R 4 2

    Passo 3

  3. Pessoal, para descobrirmos o campo magnético, vamos partir da ideia de simetria, uma vez que é um círculo. Após isso, veremos qual fórmula será a utilizada para os dois intervalos de variação do raio A imagem abaixo ajudará na visualização.

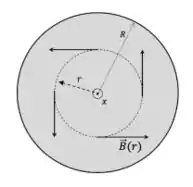
Pensando nisso, qual fórmula se encaixa perfeitamente para resolvermos?

Utilizaremos a lei de Ampère, que é dada por

∮ B → . d l → = μ 0 I

Para 0 ≤ r ≤ R :

∮ B → . d l → = μ 0 I

Escrevendo os vetores de outra forma e sabendo que d l → =   r . d θ . θ ^ , pois só há variação em teta e estamos utilizando coordenadas esféricas, temos:

∮ B . θ ^ . r . d θ . θ ^ = μ 0 I

Colocando fora da integral o que não está variando e substituindo I pela integral ∫ J → r . d A → , temos

B r ∫ 0 2 π d θ = μ 0 . ∫ J → r . d A →

Para deixarmos tudo em função das variáveis da questão, vamos resolver a primeira integral e substituir a segunda pela equação que encontramos na letra B) desse exercício.

B r ∫ 0 2 π d θ = �� 0 . ∫ J → r . d A →

B r 2 π = μ 0 .   π K r 4 2

Diferente do encontrado na letra B), o raio será representado por r ao invés de R, pois os limites de integração são outros.

Isolando o campo magnético, temos:

B =   μ 0 K r 3 4

Na forma vetorial

B → =   μ 0 K r 3 4 θ ^

Para r > R :

∮ B → . d l → = μ 0 . I

Resolvendo de maneira semelhante à anterior, temos:

B r ∫ 0 2 π d θ = μ 0 . ∫ J → r . d A →

B r 2 π = μ 0 .   π K R 4 2

B =   μ 0 K R 4 4 r

Na forma vetorial

B → =   μ 0 K R 4 4 r θ ^

Resposta

Item A ) K = A m 4

Item B ) I = π K R 4 2

Item C) Para 0 ≤ r ≤ R : B → =   μ 0 K r 3 4 θ ^ e para r > R : B → =   μ 0 K R 4 4 r θ ^

Exercícios de Livros Relacionados

Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitos anéis circulares de carga.
Se E é a magnitude do campo num ponto P situado a uma distância D de um plano uniformemente carregado com densidade superficial de carga σ . A maior contribuição para E provém dos pontos mais próximos
Duas lâminas carregadas, infinitas e não condutora, são paralelas entre si, estando a lâmina A no plano x = - 2,0m e lâmina B no plano x = + 2,0m . Determine o campo elétrico na região x- 2,0m , na re
Uma linha uniformemente carregada, com densidade linear de carga λ à 3,5n C / m 2 , está no eixo x entre x = 0 e x = 5,0m . (a) Qual é a carga total? Determine o campo elétrico no eixo x em (b) x = 6,
Uma carga positiva está distribuída uniformemente ao longo de todo o comprimento do eixo x e uma carga negativa está distribuída uniformemente ao longo de todo o eixo y . A carga por unidade de compri