Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Campo Elétrico Gerado por uma Linha de Cargas

Ver Teoria
Exercício 3412345678910111213141516171819202122232425262728293031323335363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586

Enunciado

Um fio de comprimento L (com extremidades localizadas nos pontos x = 0 e x = L do eixo x ) está carregado com uma densidade de carga uniforme λ > 0 . Todos os pontos de interesse para o problema estão localizados no plano x y ( z = 0 ).

  1. Calcule o campo elétrico E → gerado pelo fio carregado em pontos do eixo x , para x < 0 e para x > L .
  2. Calcule o potencial elétrico V gerado pelo fio carregado em pontos do eixo x , para x < 0 e para x > L .
  3. Encontre o valor do campo elétrico E → no ponto ( x = 0 ,   y = d ) para d ≫ L .

    4. Uma partícula de carga q > 0 e massa M é então colocada em ( x = 2 L ,   y = 0 ) com velocidade inicial nula. Ela se move apenas sob a ação da força eletrostática repulsiva devido ao fio. Ignore efeitos gravitacionais.

  4. Calcule a aceleração da partícula quando ela está em alguma posição x > 2 L .
  5. Calcule a velocidade final da partícula carregada quando ela está a uma distância muito grande do fio.

Passo 1

a) Pra começar, vamos pegar um pedacinho infinitesimal do fio de carga d q e calcular o campo elétrico produzido por ele através da fórmula

d E → = d q 4 π ε 0 r 2 r ^

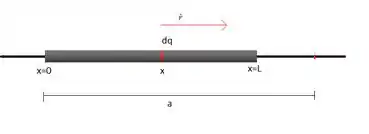
Ah, temos que lembrar também que se o fio tem uma densidade de carga λ , a carga d q pode ser escrita assim

d q = λ d r

Então a nossa fórmula do campo elétrico vai ficar

d E → = λ d r 4 π ε 0 r 2 r ^

Passo 2

Para x > L basta integrar essa expressão de a até a - L (distância entre o fio e o ponto do eixo x ).

E → = ∫ a a - L λ d r 4 π ε 0 r 2 r ^

E → = λ 4 π ε 0 1 a - 1 a - L r ^

E → = λ L 4 π ε 0 a ( a - L ) r ^

Como Q = λ L , podemos substituir.

E = Q 4 π ε 0 a ( a - L )

Para x < 0 , a resolução é igualzinha, obtendo o mesmo campo elétrico :D

Passo 3

b) A expressão para o potencial elétrico é essa

d V = 1 4 π ε 0 d q R

Como R é a distância entre um elemento de carga até aonde se deseja calcular o potencial, temos da figura que R = a - x . Além disso, vamos lembrar também que d q = λ d x

d V = 1 4 π ε 0 λ d x a - x

Agora é só integrar essa expressão entre x = 0 e x = L

V = ∫ 0 L 1 4 π ε 0 λ d x a - x

V = λ 4 π ε 0 l n a a - L

Substituindo λ = Q L :

V = Q 4 π ε 0 L l n a a - L

E assim como no campo elétrico, o potencial elétrico é o mesmo para x < 0 certo?

Passo 4

c) Beleza, nesse caso a gente tem algo parecido com essa figura

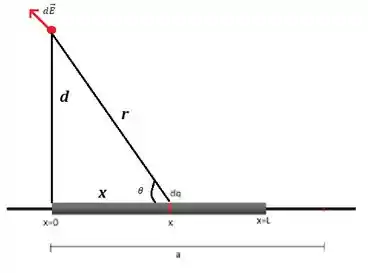
O módulo do campo elétrico nesse ponto vai ser

d E = λ d x 4 π ε 0 r 2

Passo 5

Vamos agora decompor esse campo elétrico no eixo x (horizontal) e no eixo y (vertical) utilizando o ângulo θ da figura, vai ficar assim

d E x = - λ d x 4 π ε 0 r 2 c o s ⁡ ( θ )

d E y = λ d x 4 π ε 0 r 2 s e n ⁡ ( θ )

Aplicando Pitágoras na figura, a gente descobre que r = x 2 + d ² , então

cos ⁡ θ = x r = x x 2 + d 2

sen ⁡ θ = d r = d x 2 + d 2

Substituindo nas expressões:

d E x = - λ d x 4 π ε 0 ( x 2 + d 2 ) x x 2 + d 2 = - λ x 4 π ε 0 d x ( x 2 + d 2 ) 3 / 2

d E y = λ d 4 π ε 0 ( x 2 + d 2 ) d x x 2 + d 2 = λ d 4 π ε 0 d x ( x 2 + d 2 ) 3 / 2

Passo 6

Agora é só a gente integrar as expressões de d E x e d E y de x = 0 até x = L

E x = - λ 4 π ε 0 ∫ 0 L x d x ( x 2 + d 2 ) 3 / 2

E y = λ d 4 π ε 0 ∫ 0 L d x ( x 2 + d 2 ) 3 / 2

Eu sei que essas integrais parecem bizarríssimas, mas o formulário da prova dá a resposta delas pra gente (AMÉM), segundo o formulário:

∫ x d x ( x 2 + d 2 ) 3 / 2 = - 1 x 2 + d 2

∫ d x ( x 2 + d 2 ) 3 / 2 = x d ² x 2 + d 2

Então bora aplicar isso e substituir os limites de integração, a gente vai chegar que

E x = λ 4 π ε 0 1 L 2 + d 2 - 1 d 2

E y = λ 4 π ε 0 d L L 2 + d 2

Como L ≫ d , a gente pode simplificar essas expressões assim:

E x = λ 4 π ε 0 1 L - 1 d

E y = λ 4 π ε 0 d L L 2 = λ 4 π ε 0 d

Passo 7

d) Como a partícula se movimenta apenas pela ação da força eletrostática, a força resultante que atua sobre ela deve ser:

F r = m A = q E

Ou seja

m A = q Q 4 π ε 0 a ( a - L )

m A = q λ L 4 π ε 0 a ( a - L )

Então a aceleração A da partícula vai ser

A = q λ L m 4 π ε 0 a ( a - L )

Passo 8

e) No item anterior, calculamos a aceleração, dada por

A = q λ L m 4 π ε 0 a ( a - L )

Sabemos que a aceleração é a derivada da velocidade, então

d v d t = q Q m 4 π ε 0 a ( a - L )

Logo, integrando dos dois lados:

v = ∫ q Q m 4 π ε 0 a ( a - L ) d t

Então a velocidade vai ser

v = q Q t m 4 π ε 0 a ( a - L )

Resposta

  1. E → = Q 4 π ε 0 a ( a - L ) x ^
  2. V = Q 4 π ε 0 L l n a a - L
  3. E x = λ 4 π ε 0 1 L - 1 d

    4. E y = λ 4 π ε 0 d L L 2 = λ 4 π ε 0 d

  4. A = q λ L m 4 π ε 0 a ( a - L )
  5. v = q Q t m 4 π ε 0 a ( a - L )

Exercícios de Livros Relacionados

Calcule o campo elétrico a uma distância z de um plano não condutor plano e infinito, uniformemente carregado, considerando o plano como um contínuo de infinitos anéis circulares de carga.
Se E é a magnitude do campo num ponto P situado a uma distância D de um plano uniformemente carregado com densidade superficial de carga σ . A maior contribuição para E provém dos pontos mais próximos
Duas lâminas carregadas, infinitas e não condutora, são paralelas entre si, estando a lâmina A no plano x = - 2,0m e lâmina B no plano x = + 2,0m . Determine o campo elétrico na região x- 2,0m , na re
Uma linha uniformemente carregada, com densidade linear de carga λ à 3,5n C / m 2 , está no eixo x entre x = 0 e x = 5,0m . (a) Qual é a carga total? Determine o campo elétrico no eixo x em (b) x = 6,
Uma carga positiva está distribuída uniformemente ao longo de todo o comprimento do eixo x e uma carga negativa está distribuída uniformemente ao longo de todo o eixo y . A carga por unidade de compri