Considere os dois semicírculos concêntricos de material isolante representados na figura abaixo. O semicírculo com raio tem densidade linear de carga positiva , enquanto o semicírculo menor tem raio e duas densidades lineares de carga: (positiva) para pontos com coordenada negativa e (negativa) para pontos com coordenada positiva. Os raios e as densidades lineares das duas distribuições de carga são tais que vale a relação .
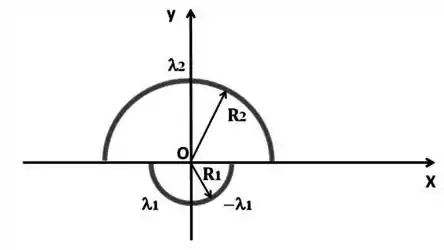
Calcule o vetor campo elétrico gerado pelo semicírculo menor no ponto (origem dos eixos e centro dos semicírculos)
Calcule o vetor campo elétrico gerado pelo semicírculo maior no ponto .
Calcule o vetor de campo elétrico resultante do ponto e escreva seu módulo.
Calcule as coordenadas da posição na qual deve ser colocada uma carga puntiforme negativa de valor , para que o campo elétrico total resultante no ponto seja nulo.
Passo 1
Vamos primeiro determinar o campo gerado pelo semicírculo menor, para isso, vamos analisar como seria o vetor campo elétrico produzido por cada metade deste semicírculo, pois temos que cada metade tem uma densidade linear diferente.
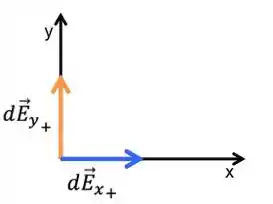
Vamos começar pela metade positiva, sabemos que o campo elétrico “sai” das cargas positivas, temos então, decompondo em e , que a componente do campo infinitesimal aponta na direção positiva do eixo , enquanto que a componente aponta na direção positiva do eixo , fica assim:
Show!
Pensando na outra metade do semicírculo, pelo fato de ela ser negativa, o campo irá apontar em direção a ela, pensando na decomposição, temos que a componente irá apontar na direção positiva do eixo , enquanto que a componente irá apontar na direção negativa do eixo , fica assim:
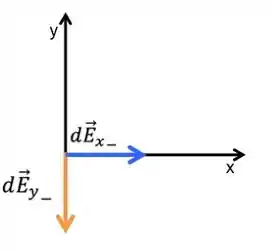
A partir das duas decomposições que fizemos, e levando em consideração a simetria, vemos que as componentes irão se cancelar, enquanto que as componentes irão se somar. Ótimo, isso significa fazer menos conta!!
Passo 2
Agora que sabemos que o campo resultante será na direção positiva do eixo , e que as componentes e tem o mesmo módulo, basta calcular uma das componentes e multiplicar por dois, se liga!
Temos que o módulo do campo infinitesimal é:
Tendo em vista que queremos apenas a componente , ou seja, , temos:
Substituindo e , temos:
Agora é só integrar, ah...não esqueça que :
O campo total será:
Bora pro próximo item!
Passo 3
Agora que já fizemos o item , esse item vai ser moleza!
Pensando da mesma maneira que no item , percebemos que ambas as metades irão produzir um campo que aponta para fora, desse modo teremos que as componentes irão se anular, enquanto as componentes irão se somar, apontando na direção negativa do eixo. A partir do módulo do campo infinitesimal, temos:
Tendo em vista que queremos apenas a componente , ou seja, , temos:
Substituindo e , temos:
Agora é só integrar, e claro, não esqueça que :
O vetor campo será:
Passo 4
Para determinar o vetor, é só somar os resultados dos itens e :
O módulo será:
Calma...nada saiu da cartola, lembre que no enunciado foi dado que !
Passo 5
Analisando o campo resultante , vemos que o campo que o anula, ou seja, o campo gerado pela carga, deve ser:
Pela relação :
Sabendo que a carga é negativa, , temos que o campo aponta em sua direção, portanto, a carga deve estar posicionada no segundo quadrante.
Além disso, pela simetria, sabemos que ela se encontra a mesma distância do eixo que ela se encontra do eixo , basta agora saber a distância da origem, pois dessa maneira saberemos o módulo do vetor posição da carga. Se liga.
Pelo módulo do vetor campo que é produzido pela carga, temos:
Substituindo o valor do módulo da carga, temos:
Agora que temos o módulo, determinar o vetor posição é fácil!
Lembre-se que só ficou fácil pois sabemos que a carga está no segundo quadrante e que as componentes devem ter o mesmo módulo!