Considere um anel circular, fino de raio , com uma distribuição de carga linear, estacionária, com carga total . O campo elétrico, devido a tal anel em um ponto de seu eixo perpendicular de simetria, com cota , definida a partir do centro do anel (conforme a Figura 1), é dado por:
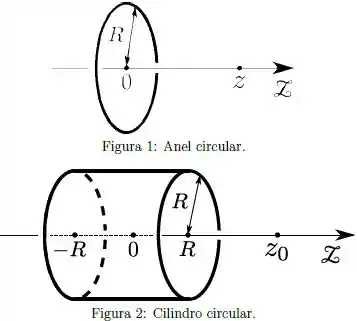
Considere, agora, uma superfície cilíndrica (aberta, ou seja, sem incluir as bases) circular, reta, de raio , e comprimento (ou altura) , com uma densidade superficial constante (homogênea e estacionária) (conforme a Figura 2).
Determine a carga total do tal cilindro.
Supondo que tal cilindro é coaxial com o eixo , com seu plano médio coincidente com o plano (conforme a Figura 2), determine o campo elétrico em um ponto do eixo , com cota .
Encontre o limite assintótico do campo do cilindro determinado no item (dependência do campo com ), para . Discuta o resultado encontrado.
Passo 1
Determine a carga total do tal cilindro.
Por definição, a densidade superficial de carga é dada por:
No entanto, como é constante, podemos reescrever a equação acima da seguinte forma:
Onde é a área superficial do cilindro. Como o cilindro não tem a base, temos que:
Onde . Logo:
Substituindo na expressão de , teremos:
Finalmente:
Passo 2
Supondo que tal cilindro é coaxial com o eixo , com seu plano médio coincidente com o plano (conforme a Figura 2), determine o campo elétrico em um ponto do eixo , com cota .
Pra começar, vamos dividir o cilindro em infinitos anéis, cada um com carga e que gera um campo elétrico em , dado pelo enunciado:
Onde é a distância do centro do anel infinitesimal ao ponto .
A carga está associada à densidade superficial de carga por:
Onde . Logo:
Agora só precisamos integrar esse cara, onde vai variar de até . Portanto:
Passo 3
Calma, eu sei que essa integral pode assustar, mas podemos resolvê-la usando uma substituição simples, se liga:
Assim, teremos:
Vamos dar uma organizada nisso:
Agora sim, podemos integrar esse cara:
Agora podemos substituir de volta:
Finalmente:
Passo 4
Encontre o limite assintótico do campo do cilindro determinado no item (dependência do campo com ), para . Discuta o resultado encontrado.
Antes de qualquer coisa, vamos ter que mexer um pouco com a expressão que encontramos do campo elétrico. Vou procurar fazer aos poucos.
Beleza, agora vamos tirar o de dentro da raiz:
Show! Agora, se fizermos , vamos ver que todas as frações dentro dos parênteses vão tender a zero, e o resultado final seria zero.
No entanto, existe um jeito de resolver o problema, que é usando a expansão que inclusive é fornecida no formulário da prova:
Assim, para o primeiro e segundo termo, respectivamente, vamos fazer:
Logo:
Agora é dar um jeito na bagunça:
Finalmente:
O interessante aqui é que na letra nós encontramos:
E se olharmos novamente a expressão do campo elétrico, podemos reescrevê-la como:
Que é justamente o campo elétrico gerado por uma carga puntiforme a uma distância da mesma. Ou seja, para , o cilindro se comporta como uma carga puntiforme.
Resposta