Considere o bastão delgado da figura, de comprimento , posicionado ao longo do eixo . Sobre o bastão existe uma densidade linear de carga dada por , onde é uma constante positiva (todas as unidades estão no SI). Um determinado ponto possui coordenadas retangulares onde .
a) Considerando a referência dos potenciais no infinito encontre o potencial no ponto .
b) Suponha agora que o potencial gerado pelo bastão no ponto seja dado pela expressão:
onde é uma constante positiva (todas as unidades estão no SI). Calcule a componente do vetor campo elétrico em a partir da expressão fornecida. Responda também se as componentes e do vetor campo elétrico em , devidas ao bastão com a densidade linear de carga original, são positivas, negativas ou nulas, sem precisar calculá-las diretamente a partir da lei de Coulomb (Sugestão: use argumentos de simetria).
Considere novamente a expressão dada no item (b), agora com os valores numéricos , e em unidades do SI.
c) Calcule todos os pontos do espaço em que a carga puntiforme pode ser colocada de modo que o potencial TOTAL gerado em tenha o triplo do valor daquele gerado unicamente pelo bastão.
Passo 1
O diferencial de potencial em gerado por um infinitésimo de carga do bastão, localizado em , é dado por
onde é a distância representada em vermelho
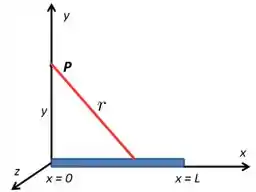
e é dada por
A densidade linear de carga se relaciona com por
Assim o potencial em será dado por
A integral acima pode ser feita substituindo , ou você já pode ter ela no seu formulário :)
Passo 2
Sabemos que a componente do campo elétrico é dada por
Já o campo na direção deve ser
Isso por que o nosso bastão está no plano , logo todo campo gerado por cada componente do bastão tem que ser um campo também contido no plano
Já o campo na direção tem que ser
ou seja, a componente deve apontar para direita.
Isso por que como nosso bastão começa em e termina em , e é positivo, todo elemento irá produzir uma componente de campo na direção apontando para a esquerda.
Passo 3
O potencial no ponto será devido ao bastão e a carga , ou seja
Como queremos que o potencial no ponto seja igual ao triplo do potencial do bastão, temos
O potencial devido ao bastão é dado por
No ponto
Em unidades do SI
Isso tem que ser igual ao potencial da carga
Assim como queremos que
Ou seja, todos os pontos que distem satisfazem a nossa condição. Esses pontos estão em uma superfície esférica de raio e centrada em
Resposta
- Pontos da superfície esférica de raio e centrada em