Dois fios retilíneos de comprimento , carregados com densidades lineares de carga e , são conectados por um fio semicircular de raio , uniformemente carregado com densidade de carga .
Devido ao campo elétrico resultante em , uma carga eletrica abandonada neste ponto é ejetada formando um ângulo com a direção dos dois fios retilíneos.
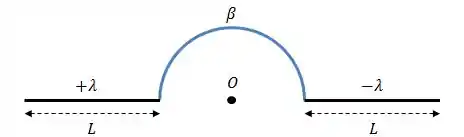
Dados: e
Determine o campo elétrico em devido a distribuição de cargas ;
Calcule a componente vertical do campo elétrico em devido a distribuição de cargas ;
Com os valores de e , determine a densidade linear em função de , e ;
Passo 1
Determine o campo elétrico em devido a distribuição de cargas ;
O primeiro passo é escrever a expressão do campo elétrico gerado por uma carga infinitesimal , dado por:
Graficamente, a ideia é essa:
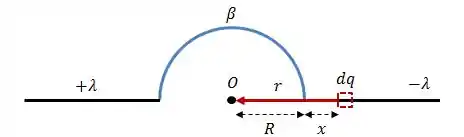
Onde:
Fazendo essas alterações:
Passo 2
Pra finalizar, temos apenas que integrar esse cara entre e :
Finalmente:
Passo 3
Calcule a componente vertical do campo elétrico em devido a distribuição de cargas ;
Tá legal que o problema pede pra calcularmos somente a componente vertical do campo elétrico devido à distribuição de cargas ... mas se analisarmos melhor, veremos que essa distribuição de cargas gera apenas um campo elétrico vertical no ponto .
Pra entendermos melhor, vamos pegar dois pontos simétricos do semicírculo e ver o campo gerado pelas cargas infinitesimais desses pontos:
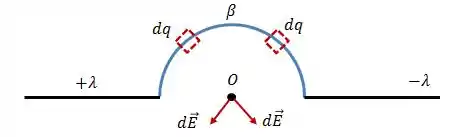
Se decompormos os vetores , veremos que eles vão se anular na horizontal e se somar na vertical. Isso vai acontecer pra qualquer par de pontos simétricos. No final das contas, teremos apenas um campo elétrico vertical.
Ok, agora podemos calcular esse campo elétrico.
Passo 4
A ideia aqui é a mesma que usamos para calcular o campo elétrico gerado pela distribuição . Então vamos começar escrevendo a expressão do campo elétrico gerado por uma carga infinitesimal , dado por:
Graficamente, a ideia é essa:
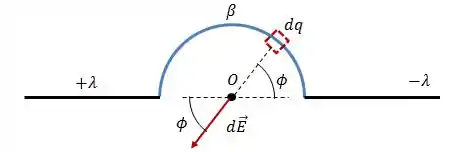
Daqui podemos tirar algumas coisas:
Assim, a componente vertical do campo será dada por:
Agora é só integrar esse cara em :
A resposta do problema é essa aqui em cima! Mas só pra não esquecermos o que falamos antes, o campo elétrico gerado pela distribuição no ponto será:
Passo 5
Com os valores de e , determine a densidade linear em função de , e ;
O campo elétrico resultante no ponto será a soma dos campos elétricos gerados pelas distribuições , e .
Os dois fios são bem parecidos, certo? Só que um fio está à esquerda de e o outro está à direita de sendo que um tem densidade e o outro tem densidade .
Em módulo faz total sentidos esses campos serem iguais pela simetria!
Agora basta definir a direção do campo do fio com densidade .
O fio da direita produz um campo que aponta na direção desse mesmo fio por que ele tem carga negativa (mesmo raciocínio do caso de uma carga pontual negativa), então o fio da esquerda produz um campo que aponta para fora em relação ao fio com densidade ! Assim os dois campos apontam para direita e são iguais
Passo 6
Quando o problema diz que uma carga colocada no ponto é ejetada formando um ângulo de com a horizontal, o que ele quer dizer, na verdade, é que o campo elétrico resultante no ponto está formando um ângulo de com a horizontal.
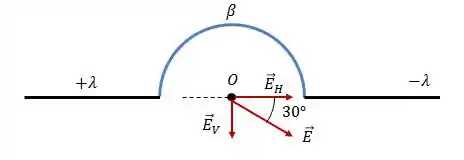
Logo:
Onde:
Portanto:
Ajeitando a bagunça:
Resposta