A figura abaixo representa uma esfera maciça não-condutora, de raio e densidade volumétrica de carga constante . Tal esfera maciça está envolvida por uma casca esférica concêntrica, também não-condutora, de raio interno e raio externo . A casca esférica tem uma carga elétrica uniformemente distribuída em toda sua extensão. A distância radial ilustrada na figura (segmento reto tracejado) pode variar no intervalo , onde localiza o centro comum da esfera maciça e da casca esférica. Além disso, uma carga pontual está fixada num ponto localizado entre a esfera maciça e a casca esférica, onde . Nestas circunstâncias, calcule:
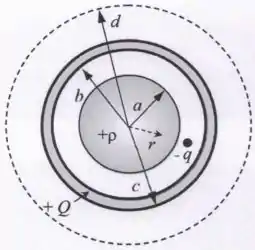
- O módulo do campo elétrico em um ponto no interior da esfera maciça, onde .
- O módulo da força elétrica total sentida pela carga que está na região onde .
- Para que valor da carga da casca o fluxo elétrico total através da superfície esférica tracejada de raio ilustrada na figura é nulo?
Passo 1
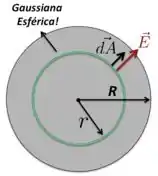
Para essa superfície gaussiana, vamos ter que aplicar a lei de Gauss
em que é a carga total líquida que está dentro da superfície fechada (superfície gaussiana) de raio .
Nesse caso, como , então a superfície gaussiana não engloba toda a carga da esfera. Por isso, como é constante, temos que
Como está na figura acima, o vetor infinitesimal de área deve sempre apontar para fora da superfície gaussiana, portanto, , que está na direção radial .
Agora, como a carga da esfera não-condutora de raio é positiva, então o campo elétrico que ela produz também aponta na direção radial e, por causa da simetria esférica do problema, esse campo depende apenas da distância até o centro da esfera. Com isso, vamos ter que o vetor campo elétrico é:
e, por isso, é paralelo ao vetor .
Jogando o que discutimos dentro da lei de Gauss, teremos:
Agora, outra informação importante, é que, como o campo elétrico tem o mesmo valor em todos os pontos da superfície gaussiana, podemos tirar da integral e reescrever o seguinte:
que simplificada, fica
que é o queríamos encontrar.
Passo 2
b) Aqui precisamos calcular a força que atua sobre a carga negativa que está na região . A força que atuará sobre essa carga tem módulo dado por
sendo que é o módulo do campo elétrico produzido pela esfera não-condutora de raio na posição onde está a carga . Portanto, o nosso próximo passo deve ser calcular o campo elétrico na região .
Para isso, vamos usar novamente a lei de Gauss. O lado esquerdo fica da mesma forma que encontramos no Passo 1:
O lado direito, que depende da carga interna contida na gaussiana, é que muda, já que superfície gaussiana () engloba toda a carga da esfera de raio . Portanto,
Juntando tudo, vamos ter o módulo do campo elétrico em é
Com isso, a módulo da força que atua sobre é dado por
O vetor da força elétrica atuando sobre ficaria escrito como:
que aponta no sentido de aproximar da carga positiva da esfera de raio , como deveria ser ;-)
Passo 3
c) Para fechar, a superfície gaussiana esférica com engloba total que podemos escrever como
sendo que o primeiro termo depois da igualdade é a carga total da esfera interna de raio .
O fluxo do campo elétrico através da superfície de raio é dado por
Para encontrarmos como deve ser a carga para que isso aconteça, temos que resolver a equação acima, que vai dar o seguinte: