A figura mostra uma barra não-condutora com uma densidade linear de carga positiva distribuída uniformemente ao longo de seu comprimento. A barra é dobrada em uma semicircunferência de raio .
O módulo do campo elétrico no centro da semicircunferência é:
Passo 1
Qual é a estratégia aqui?! Vamos começar olhando o campo elétrico gerado por um pedaço bem pequeno da barra, com carga infinitesimal :
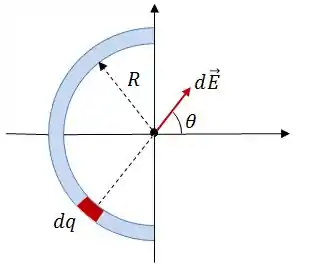
Passo 2
Como estamos trabalhando com vetor, a boa aqui é decompor esse cara usando o ângulo , onde:
Passo 3
Onde, usando a densidade linear de carga , podemos escrever a carga infinitesimal como:
Como corresponde a um pedaço infinitesimal do arco de circunferência, temos que , dessa forma:
Ao substituir na expressão do campo elétrico:
Passo 4
Pra fechar, basta integrar essas duas expressões, onde :
Arrumando a casa:
Finamente:
Resposta