Uma linha uniforme de cargas de comprimento e a carga total produz um campo elétrico a uma distância da linha ao longo da sua mediatriz que é dado pela equação: .
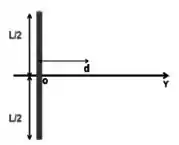
Considere agora um sistema constituído por uma calha cilíndrica isolante de comprimento , raio de curvatura , carregada uniformemente com carga total positiva. A origem dos eixos está situada sobre o eixo da calha, a uma distância da superfície lateral da mesma, e no plano mediano que corta a calha em duas partes idênticas de comprimento . A interseção da calha com o plano descreve um arco de circunferência de ângulo igual a , com , como representado na figura.
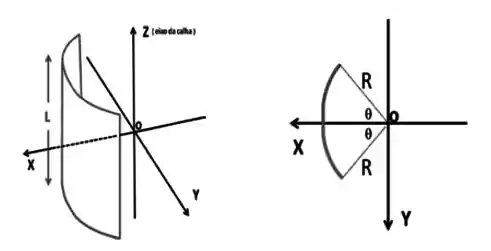
Considere a calha como constituída por fios de carga infinitesimal , largura e comprimento . Calcule a carga infinitesimal de cada fio. (A densidade superficial de carga da calha é )
Considerando que , obtenha o módulo, direção e sentido do campo elétrico gerado pela calha carregada na origem dos eixos .
Um plano infinito carregado uniformemente é agora colocado paralelamente ao plano cortando o eixo na coordenada . Nesta condição, nota-se que o campo elétrico resultante na origem é nulo.
Calcule a densidade superficial de carga do plano infinito carregado.
Passo 1
Para determinar a carga de cada fio infinitesimal, podemos pensar que cada fio possui espessura e comprimento , logo a carga infinitesimal de cada fio será:
Passo 2
Como a calha está carregada positivamente, temos que o campo na origem dos eixos aponta no sentido negativo do eixo . Isso porque cada parte simétrica da calha contribui com um campo e cada componente infinitesimal irá cancelar a componente no eixo . Cada componente vale:
Como, , temos que:
Integrando para achar o campo:
Passo 3
Para um campo infinito carregado, temos que o campo produzido por ele é dado por:
Igualando ao campo produzido pela calha, de modo à cancelar o campo na origem, temos:
Resposta