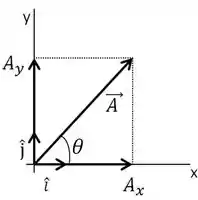
O vetor está desenhado na figura ao lado. Sobre esse vetor e com base na figura, marque a alternativa incorreta:
A.
B.
C.
D.
E.
Passo 1
Vamos analisar as alternativas, tendo muita atenção porque queremos a INCORRETA!
Passo 2
Na letra A ele fala pra gente o módulo do vetor, ou o valor numérico, que o “tamanho” daquele vetor, é o módulo do vetor é dado pela fórmula:
Então a nossa letra A está correta!
Passo 3
Nas letras B e C ele tá falando sobre as componentes do vetor nas direções e .
Vamos usar um macete: Quando a gente tem que decompor um vetor usamos o e o . De quem? Do , que foi dado pra gente. Ah mais qual é a componente que vou usar o e qual é a que vou usar ? Aí que tá, acompanha comigo:
A componete está bem COlada com o , né? Aí a gente lembra de quem? Do COsseno.
Então é
Show?
Já a componente está SEparada do . Aí a gente lembra de quem? Do Seno.
Então é
Maravilha, vimos que a B e a C estão corretas!
Passo 4
Na letra D ele tá calculando a , que é o cateto oposto/cateto adjacente. O tamanho do cateto é o tamanho da componente.
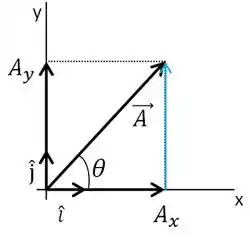
Olha ali, aquela seta azul tem o mesmo tamanho da seta , certo?
Então pra gente calcular a tangente do :
Show? Então a letra D também está correta.
Passo 5
A gente sabe que essa vai estar errada, já que todas as outras estavam certas, né? Mas vamos analisar ela direitinho.
O arco tangente é o inverso da tangente. Pode parecer confuso, mas na prática é bem simples.
Se pra calcular a tangente a gente usa um ângulo e obtem um número, no arco tangente nos vamos usar o número para obter o ângulo. Acompanha comigo:
No passo anterior nos achamos a tangente do :
Agora, pra gente calcular o arco tangente:
Opa!! Lá na letra E a ordem está errada! Portanto, a alternativa incorreta é a E.
Resposta
Alternativa E.