32) Seja qualquer curva unindo qualquer ponto na circunferência a qualquer ponto na circunferência , . Seja . Mostre que tem sempre o valor .
Passo 1
Então, resolver uma integral de linha no caso vetorial, existem, agora, três formas de resolvê-la:
1º - Forma direta.
2º - Teorema de Green.
3º - Com funções potenciais.
Aqui não precisa de muito para falar que o caminho que vamos utilizar para resolver essa integral é o mesmo, pois sabemos que uma integral sempre terá um mesmo resultado não dependendo do caminho quando existe a função potencial , sacou?
Então vamos procurar essa função potencial!
Passo 2
Pela definição de função potencial , essa função é tal que:
Como o gradiente de é:
Onde tiramos duas igualdades:
Passo 3
Com a primeira igualdade calculemos uma integral “revertendo” a derivada e voltando para a função ...
Porém repare que apareceu uma função que depende somente de ali, pois caso derivemos novamente essa função em relação à , ela desaparece por ser considerado uma “constante” perante , logo... Na integral ela reaparece, sacou?
Calculando essa integral com relação à , portanto, tomando como uma constante, faça uma mudança...
Passo 4
Basicamente essa é a função potencial, porém, como você pode ver, ainda falta uma coisa a descobrir, a função . Façamos isso utilizando a segunda igualdade...
Derivando a função que determinamos em relação à então...
Esse segundo termo de derivada é uma derivada simples, pois só depende de ...
Derivando...
E agora comparando com a igualdade número ...
Logo... A única forma dessa derivada zerar é se a função for uma constante...
Então a função potencial finalmente é
Passo 5
Para matar a charada, antes apenas lembre que com uma função potencial em mãos, calculamos uma integral de linha muito fácil tendo apenas o ponto inicial e o ponto final , pois...
Então...
Se o ponto está em qualquer ponto da circunferência de raio e o na circunferência maior...
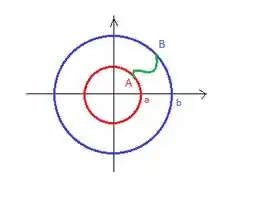
Resposta
Prova-se utilizando funções potenciais: