Seja

1. é conservativo? Por quê?
2. Calcule ,
3. Calcule , , orientada no sentido anti-horário

Beleza, essa é uma condição necessária, mas não suficiente! A outra condição para termos algo suficiente para falar que esse campo de fato é conservativo é um domínio simplesmente conexo.

Em outras palavras, é um domínio que não tenha problema de se criar curvas fechadas, pois qualquer ponto do interior dessa curva o campo funciona (é contínuo ):

O campo como pode ver, tem um problema quando , pois o não existiria nessas condições, mas em qualquer outro ponto do lado esquerdo, funcionaria.

Então nesse domínio ela é conservativa, pois aquela subtração de derivadas zerou e estamos em um domínio simplesmente conexo, sacou ?

Repara que temos aquela função , e para achar a função potencial devemos integrar essa parada, mas sinceramente a integral disso não é nada simples nem fácil de fazer, eu mesmo não faço ideia como resolver.

Então vamos ignorar a função potencial por enquanto, vamos usar as propriedades de campos conservativos para prosseguir com os cálculos:

1º - propriedade nos fala que se é uma função potencial de um campo , então

Onde e são os pontos iniciais e finais da curva!

2º - O caminho não importa, apenas esses dois pontos mesmo!

Letra b) Repara que o ponto inicial dessa parada vai ser em , esse ponto vai ser

E o ponto final vai ser em , esse ponto vai ser

Que é o mesmo ponto, então a integral de linha nessa curva vai ser , isso porque a integral de linha vai ficar, com sendo a função potencial

Letra C) Vamos começar entendendo os pontos que o problema quer: ele deu uma circunferência com centro em e raio . Ele quer que a parada tenha . Isso nos diz que a circunferência vai ser a “banda” da direita. Vai ficar algo assim

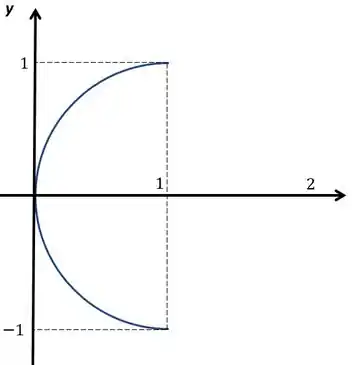
Ele vai de até .

Lembra das propriedades de campos conservativos? O caminho não importa, então vamos pegar uma reta que vai direto de um ponto ao outro, a sua parametrização vai ficar

Com

Precisamos fazer agora

A integral de linha vai ficar