Seja um campo de vetores de classe no anel Considere asseguintes afirmações:
- Se , para todo então para toda circunferência .
- Se é conservatiro em , então para todo .
- Se para toda circunferência com centro na origem, então é gradiente em A.
A(s) afirmação(ões) verdadeira(s) para todo como acima é(são):
Passo 1
Analisando (i):
(i) Se , para todo então para toda circunferência .
Essa afirmação é falsa. Observe que se trabalharmos nessa situação com uma curva aberta, o resultado dessa integral de linha pode ser diferente de zero. Observa o teorema:
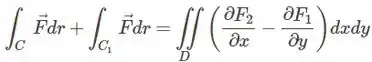
Uma vez que temos o rotacional igual a zero, temos a integral dupla igual a zero. Até ai ok. Mas não necessariamente temos uma vez que pode ser diferente de zero. (Onde é a curva utilizada para fechar a curva
Passo 2
Analisando a segunda afirmação:
(ii) Se é conservatiro em , então para todo .
Verdade! Se um campo é conservativo, temos que seu rotacional é igual a zero
.
Logo, se o campo é conservativo, sempre tereos .
Passo 3
Analisando agora a terceira afirmativa:
(iii) Se para toda circunferência com centro na origem, então é gradiente em A.
Só podemos afirmar que é gradiente se a integral sobre qualquer curva fechada der 0. Ele só fala das circunferências. Então essa alternativa está errada.