Considere o campo
Calcule a integral de linha , onde é a interseção da superfície , , com o plano orientada com crescente.
Passo 1
A curva vai ser a interseção dada pelo gráfico abaixo:
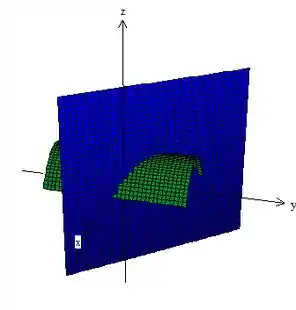
Se a gente encontrar a interseção das superfícies pra saber onde começa e termina vamos ter:
Substituindo a segunda equação na primeira:
Substituindo na terceira:
Então a curva começa no ponto e termina no ponto .
Passo 2
A primeira coisa que você tem que fazer quando ele te pedir para calcular a integral de linha
é calcular .
Passo 3
O rotacional “quase” deu zero. Na verdade, a única coisa que impediu o rotacional de dar zero foi o termo que aparece na primeira componente do campo vetorial, concorda?
Agora que vem a sacada principal do problema, que é o fato de você poder reescrever o campo vetorial da seguinte forma.
Fazendo isso, você divide esse cara em duas funções: , que eu vou chamar de e , que eu vou chamar de .
A vantagem de fazer isso é que, provavelmente, agora vai ser um campo conservativo, e isso pode facilitar a minha vida.
De qualquer forma, o problema agora é dividido em duas partes:
Passo 4
Vamos começar por .
Primeiro, vamos testar se é mesmo um campo conservativo.
Então é mesmo um campo conservativo.
Passo 5
Para problemas de campo conservativo, temos que calcular a função potencial , tal que:
Encontramos a função potencial da seguinte maneira:
Comparando as três equações para , chegamos à conclusão de que:
Passo 6
Passo 7
Agora vamos resolver .
Como a curva está sobre o plano
E sobre o cilindro
Então uma parametrização adequada é:
Passo 8
A integral de linha de sobre a curva é dada por
Agora é só substituir o que precisamos:
Portanto
Passo 9
Onde:
Logo: