Questão 2:
Seja
- é conservativo em Justifique.
- Calcule , onde é a circunferência percorrida uma vez no sentido anti-horário.
- Calcule , onde é a parte da circunferência tal que , percorrida de á .
Passo 1
Bem, para verificarmos a resposta da primeira pergunta, o que devemos fazer é observar a Teoria que nos fala que se um campo é conservativo, então ele obedece:
Onde esse nada mais são que, no nosso caso...
Calculando essas derivadas parciais, portanto...
Calculando essas derivadas com atenção na regra da cadeia...
Agora calculando a outra derivada Parcial...
Aplicando a subtração...
Olha que beleza! Deu zero, mas lembre-se: embora isso seja necessário, ainda não é o suficiente para provarmos que o campo é conservativo. Precisamos só de mais uma condição...
Passo 2
Precisamos provar que o campo é simplesmente conexo onde estamos trabalhando, saca? Simplesmente conexo significa que no domínio considerado, o campo não pode ter problemas de definição, como uma divisão por zero, ou algo do tipo. Veja:
Sabemos que o não pode ser , pois se fosse, teríamos uma divisão por em . Além disso, o logaritmo...
exige que...
Tirando essas duas condições, não temos mais nenhum problema de definição.
Como o item nos pede justamente para provar no intervalo onde , então sim! O campo é conservativo nesse intervalo, pois além de ser simplesmente conexa, a subtração ali em cima das derivadas parciais foi zero !
Passo 3
Queremos calcular a integral de linha desse campo vetorial em cima da curva fechada:
(uma circunferência de raio deslocada uma unidade a direita em )...
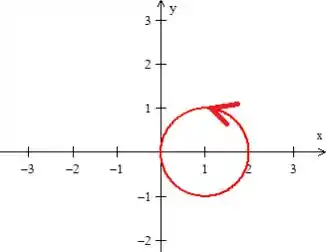
Cara, antes de sair calculando essa integral de linha aí desembestado, pensa um pouco comigo:
Estamos calculando uma integral de linha em uma curva fechada que está no domínio simplesmente conexo do campo que é conservativo, logo sem fazer conta podemos falar que...
Sacou?
Passo 4
Já é de suspeitar que o resultado dessa outra integral de linha agora em cima da semicircunferência
Não será o mesmo que o anterior, neh? Pois se não estaria muuuuito fácil. Bem, e o resultado não será justamente porque essa curva é aberta, veja:
É uma semicircunferência deslocada duas unidades a direita em e uma unidade pra baixo em ...
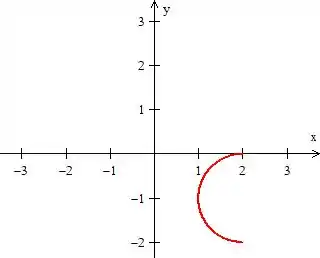
Com a orientação pedida, ou seja, do ponto ao ...
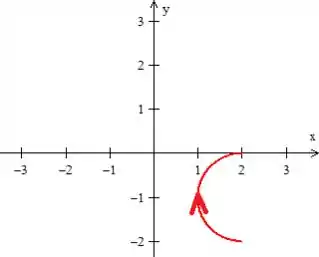
Então seu resultado não necessariamente será zero, pois ela não está fechada, mas... Como outra propriedade de um campo conservativo, a integral não depende do caminho, podemos calcular essa integral em cima dessa curva vermelha ...
Pela reta verde ...
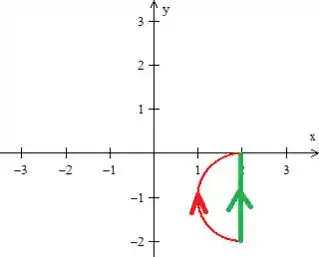
Bora?
Passo 5
Agora não tem muito por onde escapar, temos que resolver a integral de forma direta, logo precisamos...
1º - Parametrizar a reta verde .
Como ele é uma reta paralela ao eixo passando por , sua parametrização fica...
Onde varia de a .
2º - Trocar os termos do campo, pelos termos da parametrização.
3º - Calcular o termo .
Calculando...