Questão 5) Seja
- Para que valores de e o campo vetorial é conservativo?
- Para os valores encontrados no item , determine um potencial de tal que .
- Seja , . Determinar
Onde é a curva parametrizada por .
Passo 1
Ouvi conservativo??? Então a primeiríssima coisa que você tem que ver é se o campo funciona em todos os pontos do espaço. Em outras palavras, é verificar se ele é simplesmente conexo!
Pow! Olha para o nosso campo
Repare bem que ele é composto por polinômios e por exponenciais, ou seja, funciona pra qualquer ponto que a gente quiser! Sacou? Então ele é simplesmente conexo sim!
Mas a análise não acabou por aqui, neh? Bora para o último quesito...
Passo 2
Para o campo ser conservativo também, outra coisa que precisa acontecer é essa parada aqui ser verdadeira
OBS: Esse termo do primeiro membro é aquela famosa subtração que utilizamos no Teorema de Green, se lembra? e são as componentes do campo...
Derivando...
Substituindo...
Pow, veja que se e , não importa o valor de e que o resultado sempre é , tornando o campo conservativo!
Passo 3
Tá! Ele é conservativo, mas o que isso significa exatamente?
Significa que o campo possui uma função potencial que, por definição, atende a equação:
Esse segundo termo, se você não se recorda, é a gradiente da função ômega definido como sendo o vetor de derivadas parciais...
Pela igualdade de função vetorial então temos que...
Por igualdade de vetor...
O que vamos fazer aqui agora, basicamente é ressorver essas equações diferenciais e tirar o valor de (a função potencial )
Passo 4
Da primeira equação diferencial...
Podemos, grosso modo, “passar” o pra lado de lá e integrar dos dois lados...
Integrando...
Integrando com relação a agora (tome sendo uma constante)...
Veja que aparece um ! Você pode pensar nela como uma constante de integração, mas como integramos em e a função tem outra variável, a “constante” passa a depender dessa outra variável, saca? Se você ainda não estiver convencido, derive esse ômega com relação à ! Você vai reparar que a some por depender somente de !
Passo 5
Beleza, mas agora vamos resolver a segunda equação de modo análogo...
(Agora, para integrar em tome como uma constante):
Agora apareceu pelo mesmo motivo de ali em cima.
Passo 6
Veja que nos dois últimos passos, encontramos duas funções diferentes...
A resposta verdadeira vai ser uma combinação das duas da seguinte forma:
- Toda termo igual, aparece uma só vez...
- Todo termo diferente aparece também...
- As funções e não coloca, mas no lugar dela, coloca uma constante ...
Basicamente a gente já acabou, pois encontrou todas as funções potenciais de . Aí você poderia perguntar: “Todas?! Mas eu só vejo uma ”. Bem, repare que é uma constante e pode valer qualquer número real. Pra cada um eu tenho uma resposta diferente, saca?
Nesse caso, tem como de descobrir , pois o problema disse que
Logo, a função potencial pedida é...
Passo 7
Queremos agora calcular uma integral de linha
Onde o campo não é mais o anterior, pois e são diferentes, logo o campo será...
Isso é uma pena, pois esse campo não é conservativo já que mudou o e o ! Mas como ele deu a curva já parametrizada
Podemos simplesmente substituir que a solução vai vir rápida, correto?
ERRADO! Poxa, o problema não ia ser tão bonzinho assim com a gente, neh? Veja que o campo tem exponencial e quando substituir os termos e pelos da parametrização, iam aparecer coisas bizarras como exponencial de seno...
Por isso, a ideia vai ser tentar escapar para o teorema de Green:
Passo 8
Pow, mas antes vamos calcular aquela subtração do teorema pra ver se vai valer a pena mesmo, neh, pois não queremos fazer conta à toa. Mas atenção, você poderia se confundir e falar que essa subtração é , como vimos no passo 2, mas lembre-se que os campos são diferentes!!!
Sem mais delongas, bora pra conta...
Subtraindo...
Bem, esse termo simplifica muito, então vamos sim utilizar Green !
Passo 9
Show! Mas para aplicar o teorema, temos antes que verificar as condições que ele nos exige:
- Uma curva fechada delimitando a região .
- A curva tem que estar orientada positivamente (girando no sentido anti-horário).
- Campo sem singularidades.
Verificando...
Em ) Sim, a curva é fechada! Pois se você perceber, a parametrização dela
É de uma circunferência de raio e centrada na origem:
Em 2) O problema não nos fala nada quanto a orientação, onde a gente pode assumir que sim, a curva gira no sentido anti-horário:
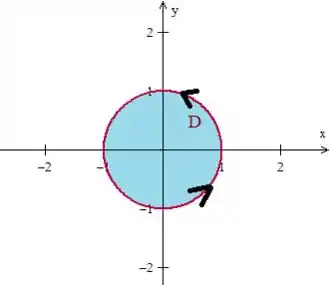
Em 3) Já vimos que o campo não tem problemas em nenhum ponto, ou seja, ele não tem singularidades.
Passo 10
Ok! Com as condições sendo satisfeitas, podemos utilizar o teorema de Green para calcular a integral de linha...
Passo 11
Para resolver a integral dupla dentro de um círculo, ora, mudança de coordenadas para as polares:
Não podemos deixar de lado os limites de e , neh? Bem, mas isso é tranquilo olhando para o círculo novamente:
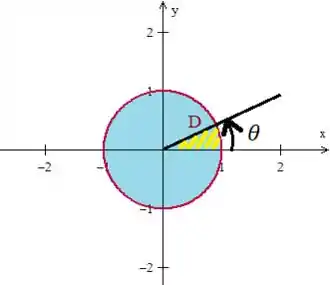
Veja que tem que dar uma volta completa:
Enquanto o raio varia da origem até o raio máximo que é...
Show, gora é só trocar a integral dupla, não se esquecendo de multiplicar a função do integrando pelo Jacobiano...
Passo 12
Por fim é só matar a integral...
Onde pelo teorema de Green, esse é o valor de integral de linha...