Seja a função definida por .
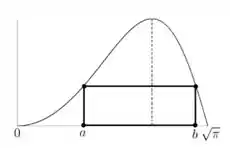
A este item um aluno deu a seguinte resposta:
Corrija a resolução do aluno e determine corretamente a área do retângulo em termos de .
Passo 1
A respota do aluno está errada, já que a área de um retângulo não tem como ser zero. O erro na resolução dele está em dizer que:
Na verdade, temos duas situações possíveis.
Ou:
De onde eu tirei isso? Do círculo trigonométrico. Lembra que pra achar um ângulo no segundo quadrante correspondente a um ângulo do primeiro quadrante, subtraímos esse ângulo de ?
Por exemplo: pra achar o ângulo no segundo quadrante correspondente a , subtraímos de , achando , que tem o mesmo seno de e o cosseno com sinal trocado (porque o cosseno no segundo quadrante é negativo).
Passo 2
Voltando ao problema, vamos escrever a área em função apenas de b.
Substituindo:
E essa é a resposta final.