Considere os seguintes sistemas carregados:
- Fio retilíneo, fino, finito, uniforme;
- Fio retilíneo, fino, finito, não uniforme;
- Fio retilíneo, fino, infinito, não uniforme;
- Anel circular, fino, uniforme;
- Bola (esférica), sólida, com densidade de carga variando só com a distância até o centro.
Qual a opção que indica, desses sistemas, aquele(s) para o(s) qual(is) pode-se aplicar a lei de Gauss a fim de deduzir uma expressão analítica explícita para o campo elétrico resultante?
- IV
- V
- I, IV
- I, V
- IV, V
- I, IV, V
Passo 1
Para podermos aplicar a Lei de Gauss de maneira conveniente, precisamos escolher uma superfície gaussiana por onde o campo elétrico é constante!
Para isso acontecer é necessário que tenhamos alguma simetria, como a esférica ou cilíndrica.
Passo 2
Um fio finito não possui campo de simetria cilíndrica, como alguns podem imaginar. É só olhar pra essa figura aqui
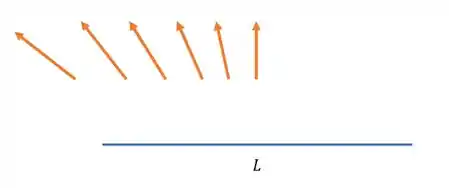
O campo logo acima do meio desse fio carregado de comprimento é vertical, mas conforme vamos andando pra esquerda ele começa a ficar mais e mais inclinado. Isso é o que chamamos de efeito de borda.
Quando o fio é infinito (ou quando o comprimento é muito grande) esses efeitos de borda desaparecem. Assim já podemos eliminar a I e a II
Passo 3
No caso IV fica difícil pensar em que tipo de superfície o campo elétrico é constante já que nesse caso não temos simetria esférica ou cilíndrica.
Ainda que possamos englobar todo o anel com uma superfície gaussiana simétrica fechada qualquer (cilindro ou esfera, por exemplo), o campo elétrico produzido pelas cargas do anel não será o mesmo em todos os pontos dessa superfície fechada. Por isso não dá para encontrar uma expressão analítica explícita para esse caso IV.
Passo 4
Por outro lado, a III nem está nas opções haha. Não conseguimos aplicação útil da Lei nela porque não sendo uniforme também não temos simetria cilíndrica do campo. Se fosse uma distribuição de cargas uniforme, aí sim teríamos esse caso.
Passo 5
Nesse caso aqui não há razão para pensarmos que o campo elétrico não seja radial e dependa somente da distância até o centro da esfera (já que a densidade também depende somente dessa distância radial).
Como o campo elétrico é radial e sua intensidade só depende da distância até o centro da esfera
Podemos escolher como gaussiana uma esfera de raio de forma que o elemento de área da esfera é
Assim fica mole aplicar a lei de Gauss
Ou seja, nesse caso é conveniente usar a lei de Gauss 😉
Resposta
Letra b