Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução à Lei de Gauss

Ver Teoria
Exercício 31245678910111213141516171819202122232425262728293031

Enunciado

Determine o campo elétrico gerado por uma esfera sólida uniformemente carregada que tem raio R e uma carga total Q , distribuída uniformemente através do volume da esfera cuja densidade de carga é ρ = Q V onde V = 4 π R 3 3 é o volume da esfera.

Passo 1

Temos aqui uma simetria esférica, isso quer dizer que o campo elétrico deve ser radial e iremos escolher uma superfície gaussiana S esférica de raio r . Na imagem da esquerda temos o caso em que r > R e na da direita temos r < R

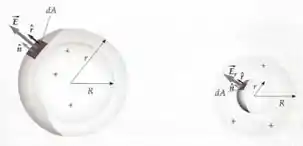
Por simetria, E n = E r e também é constante em qualquer ponto da superfície. Vamos usar a Lei de Gauss para encontrar o campo elétrico nas duas situações das imagens acima ;)

Passo 2

A Lei de Gauss é

ϕ = ∮ S E n ⅆ A = Q i n t ε 0

Como E n é constante e a área da superfície de uma casca esférica é 4 π r ² :

E r 4 π r ² = Q i n t ε 0

E r = Q i n t 4 π r ² ε 0

Agora basta avaliar essa expressão quando r < R e quando r > R

Passo 3

Quando r < R , a carga dentro da superfície gaussiana vai ser

Q i n t =   ρ V '

Onde V ' = 4 π r 3 3 , então

Q i n t = Q V 4 π r 3 3

Q i n t = Q 4 π R 3 3   4 π r 3 3

Q i n t = Q r 3 R 3

Então, o campo elétrico para r < R vai ser

E r = Q r 3 R 3 4 π r ² ε 0

E r = Q r R 3 4 π ε 0

Para r > R , a superfície gaussiana engloba toda a casca esférica, então a carga dentro dela vai ser Q mesmo

E r = Q 4 π r ² ε 0

Resposta

E → = E r r ^ onde E r = Q r R 3 4 π ε 0 ,   r < R Q 4 π r ² ε 0 ,   r > R

Exercícios de Livros Relacionados

Explique por que a intensidade do campo elétrico aumenta linearmente com r no lugar de decrescer com inverso de r 2 entre o centro e a superfície de uma esfera sólida carregada uniformemente.
Como as fórmulas para a lei da gravidade de Newton e para a lei de Coulomb têm a mesma dependência com o inverso do quadrado da distância, uma fórmula análoga à da lei da Gauss pode ser determinada pa
Uma casca uniformemente carregada com densidade volumétricaρ contém em seu interior uma cavidade esférica. Mostre que o campo no interior da cavidade é uniforme e é dado por E → = ρ d → 3 ϵ 0 , onde d
Qual é o fluxo elétrico através de um dos lados de um cubo que tem uma carga puntiforme isolada de - 3,00μ C colocada no seu centro? Dica: você não precisa integrar nenhuma equação para obter a respos
Medidas cuidadosas do campo elétrico na superfície de uma caixa preta indicam que o fluxo elétrico resultante saindo da superfície da caixa é 6,0k N ⋅ m 2 / C . (a) Qual é a carga resultante dentro da