Uma esfera sólida isolante carregada de raio R é envolvida por uma casca esférica condutora de raio interno e raio externo e carga líquida nula. As cargas da esfera isolante estão distribuídas de forma esfericamente simétrica com densidade volumétrica de cargas , onde r é à distância com relação ao centro da esfera.

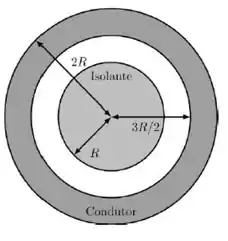
a) Se considerarmos que , qual deve ser o valor de α para que o campo elétrico a uma distância do centro da configuração seja nulo? Em outras palavras, E(4R/3) = 0.

Para os próximos itens considere que . Utilizando a Lei de Gauss, encontre a magnitude do campo elétrico E(r) nas regiões:

b) r

c) R

d)3R/2

e)2R

Considere, apenas para o item (f), que e.

f) Calcule a densidade superficial de carga σ da superfície externa da casca condutora.

A superfície gaussiana vai ter raio , e a carga interna é que acabamos de calcular, então temos:

E queremos que esse campo seja zero, então:

Simplificando tudo que podemos teremos o valor de :

Letra (b):

Vou usar sempre a lei de Gauss, então o procedimento vai ser o mesmo: calcular primeiro a carga interna e depois substituir na lei propriamente dita. Borá fazer?

A carga para é:

E a uma posição do centro a superfície gaussiana é e usando a lei de Gauss temos:

E podemos simplificar essa expressão:

Letra (c):

Agora a carga interna vai ser completa, pois a distância é maior que :

E o campo vai ser:

Letra (d):

Dentro de um condutor o campo é nulo! Sendo assim .

Letra (e): E agora para o campo é:

Já que na casca externa não temos carga líquida.

Letra (f):

A densidade de carga superficial é carga dividido por área, então temos:

Usando os valores dados de raio e densidade de cargas teremos o seguinte:

Espero ter ajudado!