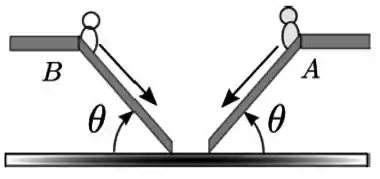
Duas escadas rolantes estão dispostas como mostra a figura. O ângulo de elevação de cada escada, em relação a horizontal é o mesmo. As escadas movimentam os degraus com velocidades constantes de mesmo módulo , medidas em relação a um referencial fixo na Terra. Em um dado instante, duas pessoas e entram simultaneamente nas escadas, como mostra a figura, e ao entrarem permanecem paradas em relação aos respectivos degraus. Seja um referencial fixo em e em translação relativa ao referencial da Terra. O módulo da velocidade de em relação enquanto e estão nas escadas é
(a)
(b)
(c) não é constante
(d)
(e)
Passo 1
Sendo e as velocidades de e em relação ao referencial da Terra, temos
Sabemos que os vetores e têm módulo e fazem uma inclinação com a horizontal. Uma boa vai ser decompor esses vetores!
Passo 2
Vamos usar o eixo apontando pra direita, com vetor unitário , e o eixo apontando pra cima, com vetor unitário :
Passo 3
Usando uma trigonometria básica, obtemos as seguintes decomposições das velocidades:
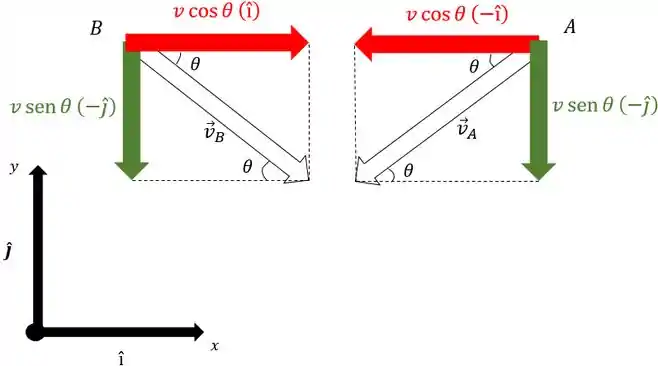
Ou seja,
Passo 4
Voltando pra fórmula do começo:
Os senos vão cortar, aí sobra
Passo 5
Show, então o módulo dessa velocidade é:
Resposta
Alternativa (d)