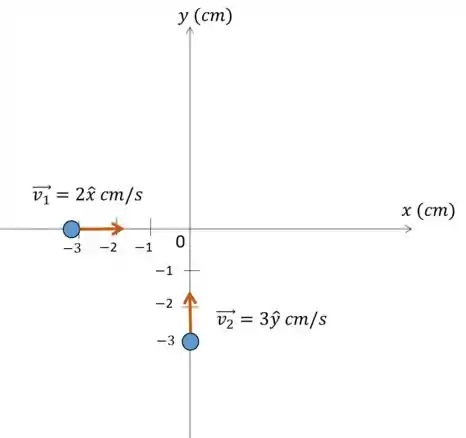
Duas partículas e se movem ao longo do eixo e , respectivamente, com velocidades constantes e . Em elas estão nas posições: , .
Esboce a situação descrita acima no plano no instante .
Escreva algebricamente (usando versores indicados no enunciado) o vetor posição de cada uma das partículas.
Determine o vetor que representa a posição relativa da partícula com respeito à partícula , como função do tempo.
Determine o vetor velocidade relativa entre essas duas partículas.
Passo 1
Colando as partículas em suas posições iniciais temos:
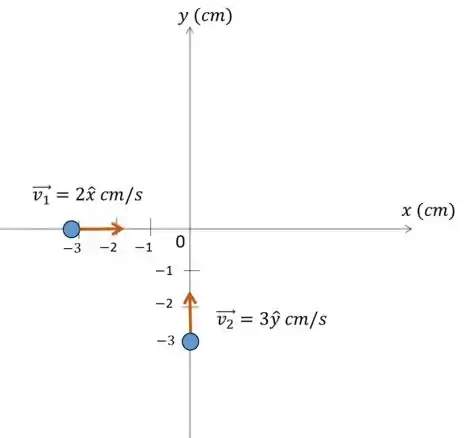
Passo 2
Vamos usar a equação da posição para determinar a posição de cada partícula.
Para a partícula temos:
Como e
Aplicando o mesmo método para , temos:
Passo 3
O vetor velocidade relativa da partícula em relação a partícula é encontrado fazendo . Analogamente, o vetor posição relativa da partícula 2 em relação a partícula 1 pode ser encontrado fazendo , Logo:
Passo 4
Como já foi dito no item anterior, basta fazer :
Resposta