Observe a figura e leia atentamente o texto:
No instante , um carro, dirigido por Bruno , se encontra na esquina de um cruzamento enquanto que outro carro, dirigido por Ângela , está em uma rua a da esquina. Bruno viaja para Norte (eixo ) enquanto Ângela viaja para o Leste (eixo ). Em relação ao solo, as velocidades de Ângela e Bruno são constantes e têm mesmo módulo de .
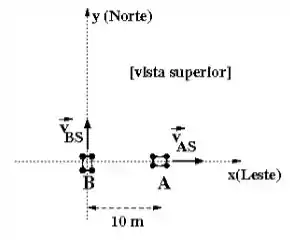
Escreva o vetor velocidade de Ângela em relação a Bruno .
Encontre o vetor posição de Ângela em relação a Bruno , em função do tempo.
Qual é a aceleração relativa de Ângela em relação a Bruno?
Passo 1
Utilizando a fórmula de velocidade relativa temos que:
Substituindo os dados sem esquecer-se de explicitar a direção das velocidades:
Passo 2
Como é constante, temos:
As posições iniciais foram dadas, e . Portanto . Assim:
Passo 3
Como é constante, então .
Resposta