[UFABC] Cálculo 1 – Lista 5 – Funções de Uma Variável – Questão 4
Uma caixa sem tampa deve ser construída a partir de um quadrado de de largura, cortando fora um quadrado de cada um dos quatro cantos e dobrando para cima os lados. Encontre o maior volume que essa caixa pode ter. Justifique detalhadamente porque o máximo existe.
Passo 1
Fala aí, pessoal! Prontos para mais uma questão sobre como encontrar um ponto de máximo na vida real? Então bora lá!
Primeiro, na nossa questão, ele nos diz que temos um quadrado de , vamos visualizar esse quadrado:
E precisamos retirar quatro quadrados das pontas desse quadrado inicial:
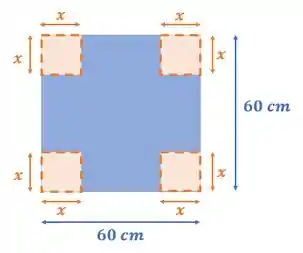
E você pode me perguntar o motivo de colocar todos os quadrados com a mesma dimensão, e eu te explico o motivo: nós precisamos dobrar as pontas que sobrarem e formar uma caixinha! Tchandam!
Vê aqui comigo:
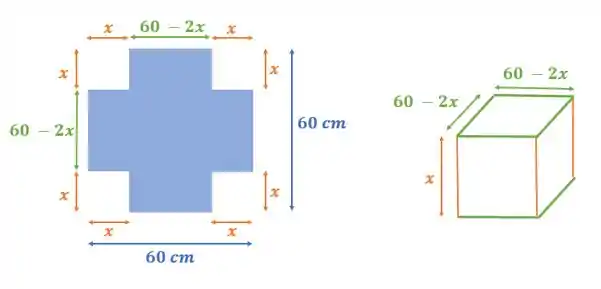
Passo 2
Passando para o próximo passo, eu espero que você concorde comigo que o volume dessa caixa é o produto das três dimensões dessa caixa, ou seja:
Fazendo esse produto, nós temos que o volume corresponde a essa seguinte função:
E como achamos qual o ponto da função corresponde ao máximo? Fazendo o teste da primeira derivada igual a zero! Tu acertou, irmão!
Passo 3
Agora vamos colocar a mão na massa de derivar esse volume aí:
E vamos igualar essa primeira derivada a zero:
Simplificando um pouquinho, vamos colocar esse pra fora da equação:
Então:
Como estamos de frente a uma equação do segundo grau igual a zero, vamos usar Bhaskara:
Então temos duas opções:
E o querido do lado daí ta achando que acabou? Não, vamos analisar o que cada um dos resultados significa, olhando pro primeiro resultado: , ele é real?
Acho que não, porque imagina um lado da caixa que mede:
Podemos ter uma caixa com lado igual a zero? Não, então vamos descartar esse resultado!
Agora pelo outro lado, vamos imaginar o segundo cenário:
Então o lado da caixa será:
Logo, podemos usar!!!
Passo 4
Por último, vamos calcular esse volume:
Substituindo o valor de que encontramos:
Temos então:
Arrasamos!!!!