UFJF, Sem Campus, Cálculo 1, AV3 - 2019.1, Questão 8
Um cilindro circular reto fechado de altura e raio das bases tem área total igual a e volume . DENTRE TODOS OS CILINDROS DE VOLUME , obtenha as dimensões daquele que tem a menor área total possível.
Passo 1
Fala galera, tudo beleza? Vamos para mais uma questão de cálculo 1. Essa é bem clássica, pois é uma de otimização.
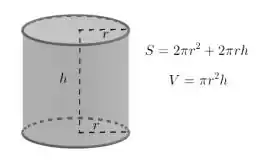
Nosso objetivo é descobrir qual é a altura e raio das bases do cilindro de menor área que tem volume igual a . E aí como fazemos isso? Alguma idéia? Bem primeiro, vamos escrever a equação da área de um cilindro. Felizmente o enunciado já diz qual é essa equação, temos que
Mas não sabemos como otimizar essa função, pois ela tem duas variáveis. Então o que podemos fazer? Ora, temos uma restrição no volume do cilindro. O enunciado diz que tem que ser . Mas o volume de um cilindro é fácil de calcular, é dado pela fórmula
Ou seja, podemos obter uma relação entre e . Então temos:
Podemos substituir esse valor na equação da área, então temos:
Substituindo
Agora temos como otimizar em relação a
Passo 2
Chegamos a conclusão que a nossa função de área do cilindro levando em consideração a restrição de volume é dada por
Agora podemos minimizar essa função. E como fazemos isso? Deriva e iguala a zero! Então temos
Pela linearidade da derivada
Quando essa derivada é igual a zero?
Ou seja, se é ponto crítico. Para ser ponto de mínimo basta verificarmos a segunda derivada.
Ou seja, a segunda derivada é sempre positiva, logo temos uma função de côncava para cima. Então o ponto crítico é um ponto de mínimo!
Isto é minimiza a área do cilindro. E como
Logo os que minimizam a área do cilindro são
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento acima