1) Seja a região limitada do plano, compreendida entre a parábola e o eixo . Considere um trapézio isóscele contido em com as seguintes propriedades:
- A base maior é o segmento do eixo ;
- Os vértices da base menor também estão situados no gráfico da parábola (ver figura abaixo)
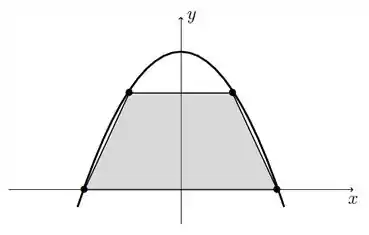
Qual a maior área possível que este trapézio pode ter?
Passo 1
Partiu então. Pra começar, vamos pensar no seguinte: como queremos otimizar uma área, precisamos saber a expressar ela primeiro! Como todo bom trapézio, a área vai ser:
Onde é a base maior, a base menor e a altura. Opa, temos três variáveis aí! Pra gente conseguir otimizar vamos ter que escrever como uma função de uma variável só! Então não tem jeito, próximo passo é relacionar as variáveis!
Passo 2
Agora pensa aqui comigo, a base de baixo é fixa, não é? Então já temos um dado do enunciado que da pra por na fórmula da área. Se a base vai de então:
Show de bola, mas falta coisa ainda. Nota agora o seguinte. Se a base de baixo ta fixa e a de cima não, mover a base menor pra cima ou pra baixo é o que faz mudar a área do trapézio! Veja que pra qualquer altura que eu escolher da base menor, é possível estabelecer um pono tal que:
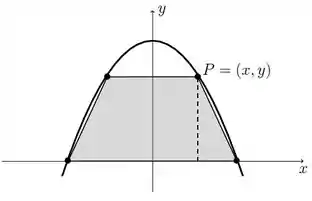
Ai você vai me perguntar: ué mas como isso ajuda a gente? Pensa comigo, se o ponto tem coordenada e está em cima da curva, a altura do trapézio vai ser exatamente a altura do ponto! E logo:
E pela simetria do problema, o outro ponto de interseção da base menor com a curva vai ser: . Opa! A distância entre esses dois pontos, que é exatamente a base menor , só pode ser então:
Fazendo a distributiva:
Passo 3
E agora chegamos na parte boa! A parte que a gente efetivamente otimiza! Pra isso, agora que sabemos como uma função de uma variável só, pra otimizar, basta derivar e igualar a zero
Fazendo Bháskara, temos:
E logo:
Como a gente não pode escolher valores negativos de , já que ele é uma grandeza física, o único ponto crítico que encontramos é:
Pra checar se ele é de máximo mesmo, vamos ver o valor da área na fronteiras. O é metade da base menor , certo? Sendo assim:
E testando o valor da área nas fronteiras e no ponto crítico, temos:
Beja bem, a área era , cresceu para e decresceu pra zero! Então ta fechado! O ponto é de fato um ponto de máximo da função e logo a maior área que o trapézio pode ter será:
Ufa! Cabamos hahaha