Seja a curva parametrizada espacial
a) Calcule duas equações implícitas para a imagem de
b) Esboce a imagem de
c) Calcule
d) Prove que onde é o campo espacial
Passo 1
Letra a)
Sendo e podemos fazer:
Da relação trigonométrica fundamental temos que , então
Sabemos da parametrização que então temos que:
Apresentando ela como função implícita temos:
As duas equações implicitas são:
Passo 2
Lebra b)
Da equação teriamos uma elipse se estivéssimos no . É fácil ver que é uma elipse pois ela é parecida com a equação da circunferência so que os coeficientes de e não são iguais. Nesse caso temos o eixo maior com tamanho e o menor com tamanho 1.
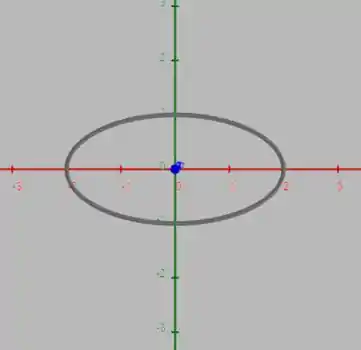
Mas como estamos no , o que acontece é que como na nossa equação o não aparece, significa que a equação é válida pra qualquer valor de . Assim o que acontece são infinitas elipses ao longo de formando um cilindro
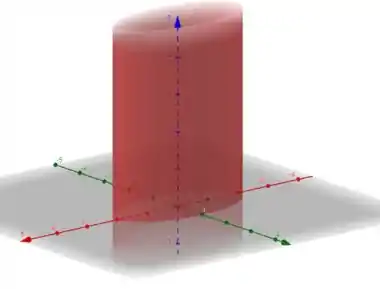
Passo 3
Para a equação temos um plano.
Imagem
Nossa curvá será então a intersecção da elipse com o plano. Portanto o esboço será algo assim:
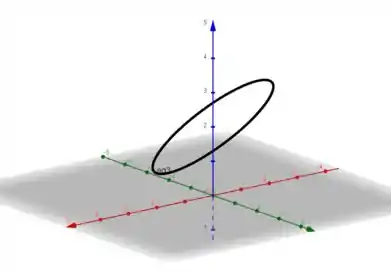
Passo 4
Letra c)
A integral que a questão está pedindo é uma integral de linha de uma função escalar ao longo da curva .
Podemos calcular ela dessa forma aqui:
Onde
E
Que é o módulo da derivada da parametrização da curva.
Resolvendo para o da questão:
Usando que
Substituindo na integral de linha e considerando que
Para resolver essa integral vamos fazer uma mudança de variável simples:
Perceba que nossos limites de integração são iguais, então nem precisamos resolver essa integral, o resultado é zero
Passo 5
Passo 6
Letra d)
Vamos usar a dica que o problema nos deu. Qual o nome do campo que quando fazemos sua integral de linha, o valor independe da curva? É o nosso famoso campo conservativo!!!! Sabemos também que o valor dele é o valor do potencial associado a esse campo aplicado no ponto final menos o potencial aplicado no ponto inicial.
Se temos uma curva fechada, então . Dessa forma a integral de linha da .
Passo 7
Vamos começar vendo se a nossa curva é realmente fechada.
Substituindo os extremos valores que assume na curva
Para
Para :
Assim podemos ver que a curva é fechada.
Passo 8
Falta agora vermos se o campo é conservativo que assim vamos ter que a integral de linha desse campo na curva é já que essa curva é fechada.
Para um campo ser conservativo ele precisa:
1) Estar bem definido no seu domínio, ou seja, não ter indeterminações tipo divisão por zero, raiz de número negativo, etc.
2) Ser irrotacional
Passo 9
Olhando para o nosso campo, podemos ver que que ele não possui indeterminações então nossa primeira condição está satisfeita
Falta agora ver se ele é irrotacional. Vamos calcular seu rotacional e se der igual a 0, ele é irrotacional
O rotacional de um campo é o produto vetorial do operador (nabla)
Vamos agora calcular então o rotacional de
Ufa! Nosso rotacional deu zero.
Então com a afirmação de que o rotacional de é zero e que a curva é fechada, temos que:
Passo 10
Resposta
Letra a)