Dois pequenos alto-falantes são ligados (em fase) à mesma fonte de sinal. Os alto-falantes estão separados por uma distância de 3,0 m. Um observador se encontra no ponto X, com o ouvido na mesma altura dos alto-falantes e em frente de um deles, a uma distância de 4,0 m, como mostra a figura. Se os sons emitidos pelos alto-falantes têm a mesma amplitude, a intensidade do som ouvido pelo observador é a maior possível quando o comprimento de onda é:
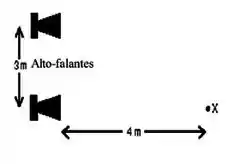
a) 1 m;
b) 2 m;
c) 3 m;
d) 0,75 m;
e) 4 m;
Passo 1
Dá uma olhada aqui:
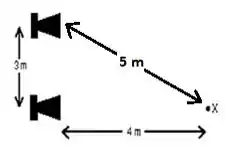
Show? Esse 5 que eu coloquei ali é porque isso tá formando um triângulo retângulo pitagórico.
Passo 2
O som ouvido pelo observador vai ser o maior possível quando rolar uma interferência entre os sons emitidos, e essa interferência for totalmente construtiva! Tem uma fórmula pra isso:
E m = 0, 1, 2, 3...
vai ser a diferença entre as distâncias do observador às fontes:
Substituindo:
Se a gente for substituindo m, vamos achar vários valores diferentes de que resolvem o problema.
Mas, no caso, o único que tem nas alternativas é pra m = 1. Graças a Thor!
![]()
Resposta
Letra A.