Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Interferência de Ondas Sonoras

Ver Teoria
Exercício 213456789101112131415161718192021222324252627282930313233343536

Enunciado

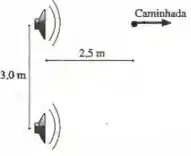
Você está parado 2,5   m diretamente à frente de um dos dois alto-falantes mostrados na figura. Eles estão afastados por 3,0   m de distância e emitem, em fase, um tom de 686   H z . À medida que você se afasta perpendicularmente ao alto-falante, a que distâncias do alto-falante você escuta um mínimo de intensidade sonora? A temperatura ambiente é 20 ° C .

Passo 1

Quando temos uma questão pedindo máximos ou mínimos, temos que usar as equações de interferência, no caso de interferência destrutiva, temos:

m + 1 2 = Δ L λ

Vamos começar determinando o comprimento de onda λ . Temos que f = 686   H z e v = 340   m / s , portanto:

v = λ . f

340 = λ . 686

λ ≈ 0,5   m

Passo 2

Agora que temos o valor de λ , vamos determinar para que valores de Δ L temos mínimos:

m + 1 2 = Δ L λ

Substituindo os valores, temos:

m + 1 2 = Δ L 0,5 = Δ L 1 / 2

m + 1 2 = 2 Δ L

1 2 ( 2 m + 1 ) = 2 Δ L

Δ L = 1 4 ( 2 m + 1 )

Temos então que os mínimos ocorrem para:

∆ L = 1 4 ;   3 4 ;   5 4 ;   7 4 …

ou ainda

∆ L = 0,25 ; 0,75 ; 1,25 ; 1,75 …

Passo 3

Vamos agora determinar Δ L para a situação inicial, para sabermos qual será o próximo mínimo!

Δ L = 3 2 + 2,5 2 1 2 - 2,5

Δ L = 1,4   m

Logo, o próximo mínimo ocorre para Δ L = 1,25   m , pois, podemos ver que Δ L diminui à medida que o ouvinte se afasta do auto-falante. Uma boa forma de ver isso é pensando no limite em que a distância é grande, nesse caso, temos que o ouvinte está praticamente à mesma distância dos dois alto falantes.

Seja d a distância entre o ouvinte e o alto falante que está na sua frente, temos:

Δ L = 1,25 = 3 2 + d 2 1 2 - d

d ≈ 2,98   m

Fazendo o mesmo mimimi para os próximos mínimos, temos:

  • Δ L = 0,75   m

    • 0,75 = 3 2 + d 2 1 2 - d

    d ≈ 5,6   m

  • Δ L = 0,25   m

0,25 = 3 2 + d 2 1 2 - d

d ≈ 17,9   m

Resposta

d ≈ 2,98   m   ;   5,6   m   ;   17,9   m

Exercícios de Livros Relacionados

A figura mostra duas fontes pontuais F 1 e F 2 que emitem sons de comprimento de onda λ = 2,00m . As emissões são isotrópicas e em fase; a distância entre as fontes é d = 16,0m . Em qualquer ponto P s
Uma onda sonora senoidal se propaga no ar, no sentido positivo de um eixo x , com uma velocidade de 343 m / s . Em um certo instante, a molécula A do ar está em seu deslocamento máximo no sentido nega
Na figura abaixo temos as ondas sonoras A e B , de mesmo comprimento de onda λ , estão inicialmente em fase e se propagam para a direita, como indicam os dois raios. A onda A é refletida por quatro su
Duas ondas sonoras, produzidas por duas fontes diferentes de mesma frequência, 540H z , se propagam na mesma direção e no mesmo sentido a 330m / s . As fontes estão em fase. Qual é a diferença de fase
Na figura, um som com um comprimento de onda de 40,0c m se propaga para a direita através de um tubo que possui uma bifurcação. Ao chegar à bifurcação, a onda se divide em duas partes. Uma parte se pr